Grunden til at jeg ville have Jensen til at indsætte 25% var at hans brugerflade ville tilføje nedenstående til ovenstående IRR-formel, for hver udbytte.

hvor X er den indsatte værdi og IRRX er intern rente, med alternativt aktiv.
Dvs. hvis X>IRRX vil brøken bliver over 1 og modsat.
Når de nærmer sig hinanden vil brøken nærme sig 1 og tilbage i ligningen er beregningen af den sande IRR.
Jensen skrev:
Jamen du kan jo ikke bare sætte 25% ind. Giver jo ingen mening. Hvor kommer det til fra? Hvis du sætter 25% ind, så ja, så går afkastet mod 25%, og hvis du sætter 100% ind går afkastet mod 100%, men det har jo intet med Pepsi at gøre hvad du investerer udbyttet i, med mindre det netop er Pepsi.
BlissY skrev:Det giver altså ingen mening det meste af det du skriver Junior.
Det er let at se, at du er ved at lære noget meget basic intern rente beregning. Din sammenkobling med de 25% i banken, giver dog absolut ingen mening.
Alexanderbp skrev:Det giver ingen mening Junior. None.
Du vil investere i Pepsi også geninvestere udbyttet i en indlånskonto som giver 25% rente siden 1980? Og det vil du se IRR-afkastet af?
Derudover, så tror jeg du har misforstået hvad interpolering er. Du kan godt løse intern rente, men du kan ikke interpolere den...
Jensen, Blissy og Alexanderbp:
Kan I se at det giver mening nu, i hvert fald matematisk
Alexanderbp skrev:
Igen, du har misforstået hvad interpolering er.. Det har intet med trial and error og gøre. Du tænker på optimization.
https://en.m.wikipedia.org/wiki/Interpolation
Altså, det er jo en ligning med kun en ubekendt. Den kan du løse selvom det er rigtig træls. Personligt ville jeg nok bare bruge en optimizer (root-finding) til at løse det (ligesom teksten du fremhæver skriver).
Uha - ja, der er kun 1 ubekendt, men den (kan) findes i 160 dele af ligningen, hver opløftet i hver deres potens, så det er altså ikke ligetil.
Jeg heller ikke din optimizer 'løser' det, men også blot approksimerer:
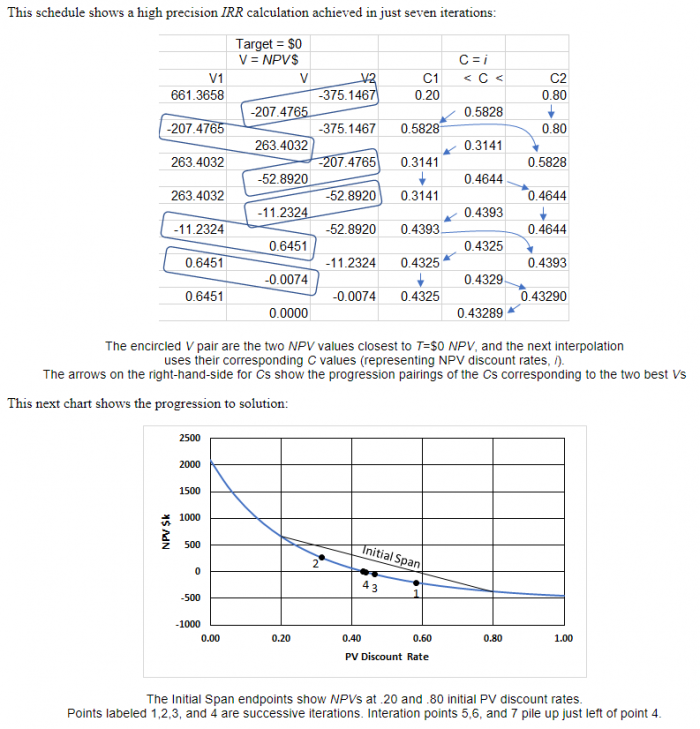
Her kan du se interpolation i aktion (jeg finder nogle flere punkter, før jeg interpolerer)

prangstar skrev:
Det er taget fra Bloomberg, og dermed de mest valide tal du kan få.
Ja - men der manglede stadig beregning for intern rente!
PS: Jeg er stadig ikke sikker på at jeg har regnet rigtigt (eller har fejl i data) så jeg håber stadig på at Jensen vil dele et screenshot mere
PPS: Investeringen er bedre end 25% i banken SÅFREMT den finansieres dyrt (har høj kapital-omkostning) - f.eks. kan investeringen i pepsi finansieres fordelagtigt, med en kassekredit på 27% (hvilket 25% i banken, selvfølgelig ikke kan)