Differential regning - brug for hjælp :)

Hej,

Det er sikkert ganske simpelt, men nu har jeg søgt gennem min bog, frividen og google, og synes simpelthen ikke jeg kan finde nogen form for løsning. Jeg er ikke rigtigt inde i differential regning endnu, så er en del jeg ikke forstår :)

Jeg ved at f(x)=e^x
Jeg ved at f´(x)=e^x
Jeg ved at e = 2,71828

Opgaven lyder
x = 5,0

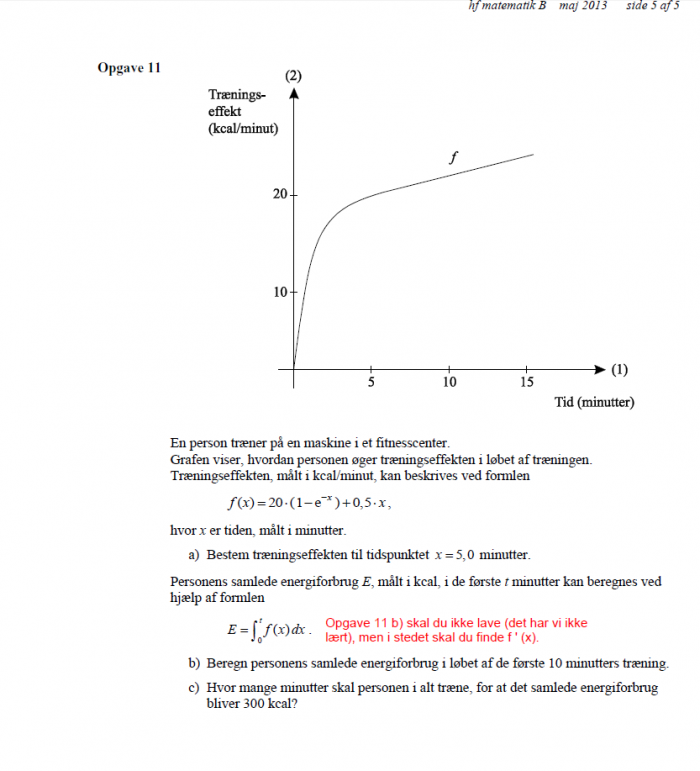
f(x) = 20*(1-e^-x)+0,5*x

Burde jo være simpelt nok, men hvad dælen skal jeg med -e^-x

Hvordan kan f(x)= e^x og f(x) = 20*(1-e^-x)+0,5*x ?? sikker på du har skrevet opgaven korrekt op?

Hvis x er lig 5, og du skal løse ligningen, så er det vel bare at sætte 5 ind i ligningen?

Så giver det et tal... Der er så vidt jeg kan se ikke noget med diffentiering i den opgave?

f(5) = 20*(1-e^(-5))+0.5*5 ?

Jeg går ud fra, at det øverste bare var et forsøg på at skrive en regneregel ind... Ikke at det er en del af opgaven...

Hvad skal du finde?

ahh ja giver meget god mening. Er målet med opgaven at finde f(5) eller f´(5) eller

Åh, du skal bare finde den afledte df/dx?

Altså, jeg skal blot finde tidspunktet 5 minutter på grafen, og gå ud af y aksen, så det er suuuuper simpelt.

Jeg gjorde som Zaphod og 20*(1-e^(-5))+0.5*5'ede, men der er noget åbenlyst jeg misser/ikke forstår, siden "((22.5*(e^(5)-0.88888888888889))/(e^(5)))" jo nok ikke er svaret på mine bønner :)

Kan jeg indsætte 2,71828 på e's plads ?

e ER 2.71828 (og nogle flere decimaler), så om du gør det eller ej, så giver det det samme...

e^(-5) = 0.00673794699

20*(1-0.00673794699)+2.5 = 19,8652410602 + 2.5 = 22,3652410602

Så det er mit resultat ved at indsætte 5 i ligningen... Men ved stadig ikke helt, hvad opgaven går ud på :)

Er det en snydeopgave? Tidspunktet: "5 minutter inde på grafen" vil jeg intuitivt sige er 5 minutter :D

ja

Jeg er ikke helt med på, hvad der spørges om i opgaven... Men så har du da et resultat, du kan prøve at se om det giver mening :)

Zorro

Thaaanks, tror jeg havde fået bildt mig selv ind at det var et nogo!

Altså, opgaven lyder på at jeg har en graf over en træningssession, og jeg skal så finde træningseffekten efter 5 minutter. Det svarer meget fint at den ligger på 22/minuttet, så jeg skulle blot plotte tallene ind :) Tak.

Okay - Super :)

Altså, det var bare første del af en lille opgave - tror det kommer nu, jeg havde blot problemer med at få løst e :)

Lige et lille spørgsmål mere.

omkring 0:35 laver hun -9x om til -9.

Hvordan kan hun bare slette x? :)

frividen.dk/default.aspx?catid=efe0c749-68f5-4665-9f91-161729a62fb2&tabid=67

og er:

f(x)=20*(1-e^-5)+0.5*x
f´(x) = 20*(1-5*e^-6)+0.5*x

korrekt?

Hvis f(x)=20*(1-e^-5)+0.5*x så er f´(x) = 1/2. Du differentierer ikke e^-6 på samme måde som x^-6 (hvilket det ligner du har prøvet).. Du differentiere kun led med x i denne ligning ( f(x) ) dermed kigger vi kun på 0.5x hvilket giver 0.5.
De andre led udgår simpelthen da de fungerer som konstanter..

Mht at "hun" laver -9x om til -9 har jeg heller ikke forstået denne opgave og hvad det egentlig er du spørg om, men det er vel indlysende at tro at -9x er blevet differentieret hvilket så giver -9 ...

Altså, har en opgave med en graf der viser en træningssession, hvor xaksen er minutter og y aksen er kcal/min forbrændt.

Jeg skal nu finde ud af hvor længe der går før jeg har forbrændt 300kcal

f´(x) = 20*(1-5-e^-5)+0.5 = 300
f´(x) = 20*(1-5- 2.71828^-5)+0.5 = 300
d=b^2-4*a*c
d=1,493^2-4*20*0,5
d=2,23-80*0,5

Hvad gør jeg forkert?

Kan du ikke scanne opgaven ind?

Jeg er sikkert på, at der mangler noget information.

Er f(x)= 20*(1-e^-x)+0,5*x den funktion, som beskriver forbrændingen?


Mvh.

sannih

Hvorfor vil du udregne Diskriminanten ? Prøv evt at oploade opgaven som billede..

Forvirrer mere end det hjælper...

Du kan jo slet ikke udregne en diskriminant, det er jo ikke en andengradsligning.

Sannih - Fattede jeg heller ikke, men gjorde hende i videoen, og så mig blind på det :)

Beklager, glemte at rette til :)

EDIT: Forkert ligning...

a) er korrekt

b) f´(x)= 20*e^-x + 0,5

c) kan nemt laves vha. integration, men jeg kan ikke se, hvordan du skal kunne lave den, da din lærer skriver, at i ikke har lært det.

I øvrigt enig med sannih i b)

Kan godt ske jeg tager fejl, men får b) f´(x) =((e^x+40)* e^-x) 2.
Opgave 3 kan sagtens laves, men ved ikke om du gider lidt kompliceret udregning? Jeg får den til =80 min. Skriv hvis du vil have udregning..

80 minutter er i hvert fald forkert... Det giver ikke meget over 15 minutter (ved at kigge på grafen - har ikke regnet på det)

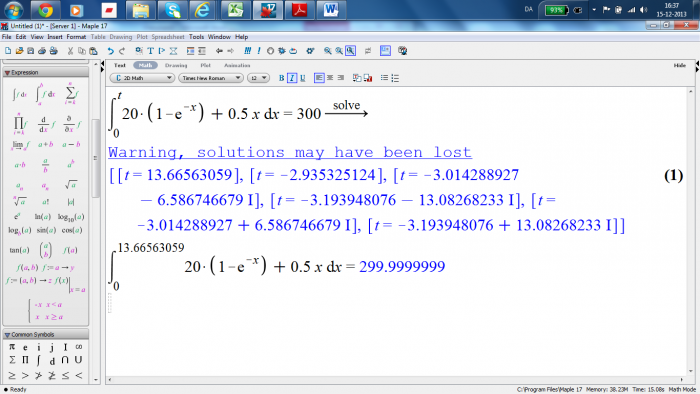
Svaret på c er 13,67 min.

Den ligning, som du opstiller, holder ikke Zorro, så skulle effekten være konstant.

b) har jeg udregnet således...


f(x) = 20*(1-e^-x)+0,5*x

vi differentierer 20*(1-e^-x) og får "20 gange det indre differentieret", så det indre differentieret giver:

- Konstanten forsvinder og så differentierer vi -e^-x, som giver -e^-x*(-1) = e^-x

Dvs 20*e^-x og så differentiere 0.5x, hvilket giver 0.5...

Facit: 20*e^-x + 0.5

sannih skrev:
Svaret på c er 13,67 min.

Den ligning, som du opstiller, holder ikke Zorro, så skulle effekten være konstant.

Hold kæft, hvor kommer jeg ikke til at forstå det her :)))

Prøver at gennemskue hvad i skriver, ty guys!

Tastefejl :).. Får også c til at være 13,67.. Integrer f(x) fra 0 til t og sæt lig 300, find så t=13,67.

@ kentkay

Jeg tror, at din lærer har lavet en bøf. Det samlede energiforbrug svarer til arealet mellem x-aksen og grafen, og det finder du vha. integralregning, som du ikke har lært.



@ Zorro

Din udregning af f´(x) er korrekt, jeg brugte bare Maple :-)

Jeg håber, at nedenstående billede kan læses.

Jeg tror at jeg har brug for bedre at forstå hvad a, b og c egentligt står for i en graf.

Jeg har en +/-/+ graf med f´(x)=3x^2-1,5*x+3

Men hvad betyder det egentligt? Altså, helt konkret, hvad er hvilke tal?
Synes min mat bog er sindsygt forvirrende, fordi den bruger så mange trekanter og jeg skal komme efter dig, og det møder jeg sleeet ikke i opgaverne.

Hey, har prøvet lidt nu.

a) Vi kender funktionen f(x) = x^3-1,5x+3
f´(x)=3x^2-1,5*x+3

b) f´(1)=3*x^2-1,5*x+3
tangents: Vi ved at x0 = 1, da (1, f1)
a = f´(1) = 3*1^2-1,5*1+3 = 4,5
y0 = 1^3-1,5*1+3 = 2,5
y– y0 = a(x – x0) = y-2,5=4,5(x-1)
y = 4,5x-2

Nogen der umiddelbart kan sige om jeg er ved at komme lidt efter det? :)

Det hjælper på det...

a) f'(x) = 3x^2-1.5 (hvis du har skrevet opgaven korrekt op :) )

Uddybende:

Vi tager ét led af gangen:

x^3 differentieret giver 3x^2
-1.5x differentieret giver -1.5
3 differentieret giver 0

Derfor 3x^2-1.5

Hvad gør at x+3 forsvinder ? :)

Ty - må lige få styr på det lort, burde være ligetil.

x+3 "forsvinder" ikke...

Du deler det op i led... Ledene adskilles af + og -... Ikke af gange...

Dvs der deles op således:

f(x) = x^3-1,5x+3

Så har du 3 led i alt... "x+3" er ikke i samme led...

Først det røde led:

x^3 differentieret giver 3x^2 (som du ganske rigtigt har... hvad gjorde du der? du trak potensen ned foran og trak 1 fra i potensen, ikke? det gør du bare i næste led også)

Næste led - det blå led:

-1.5x differentieret giver -1.5 (-1.5x er det samme som -1.5x^1... så du gør det samme som før og trækker potensen ned og trækker 1 fra... så får du (-1.5*1)x^(1-1) = -1.5x^0... og noget opløftet i 0 er = 1... Så der står -1.5*1 = -1.5)

Sidste led - det grønne led:

3 differentieret giver 0 (en konstant differentieret giver altid 0 - det forvirrer sikkert mere end det gavner at forklare hvorfor... det er lettere bare at huske det :) )

Tak for det!

Fedt i gider hjælpe en mand i nød :)

Har prøvet igen:

f´(1)=3*x^2-1,5
tangents: Vi ved at x0 = 1, da (1, f1)
a = f´(1) = 3*1^2-1,5 = 1,5
y0 = 1^3-1,5 = -0,5
y– y0 = a(x – x0) = y-0,5=1,5(x-1)
y = 1,5x-1

Hvilket punkt er det, vi prøver at finde tangenten i?

EDIT: Gætter på, at det er i (1;2.5) ud fra udregningen... Kigger lige på det :)

(1, f(1))

Jeg kan ikke huske udregningerne fra tangens i hovedet... Men 1.5x+1 lyder rigtigt... Kan du få det til at passe med det? :)

Altså PLUS 1 i stedet for MINUS 1

f´(1)=3*x^2-1,5
tangent: Vi ved at x0 = 1, da (1, f1)
a = f´(1) = 3*1^2-1,5 = 1,5
y0 = 1^3-1,5*1+3 = 2.5
y– y0 = a(x – x0) = y-2,5=1,5(x-1)
y = 1,5x+1

Sådan der, tror jeg... Hvis jeg skal gætte, for husker ikke formlen i hovedet, men ud fra dine udregninger, så er det nok noget i den retning :)

Fuck, det var jeg jeg havde i starten :)

Så det skal altså være før vi differentiere.

Det sidste er bare mit gæt... For det passer med resultatet... :D

Jeg kan ikke huske formlerne, men når man rammer det rigtige resultat, så er der da en chance for, at det er rigtigt :P

Wow . Og jeg har nogle gange svært ved at hjælpe tøsen som går i 7. :)

Mice

Det er som sådan nemt nok, da vi trods alt har en lommeregner man bare kan trykke ind på, det svære er også at forstå det - det jeg forsøger mig lidt på :)

Tangentligningen: y = f´(x0)*(x-x0)+f(x0) = 1,5*(x-1) + 2,5 = 1,5x + 1

Skal lige have tjekket en mere fortsættende opgave :)

Samme opgave. Ligningen er nu f´(x)=1,5

f´(1.5)=3*x^2-1,5
tangents: Vi ved at x0 = 1,5, da (1,5 f1)
a = f´(1,5)=3*1,5^2-1,5 = 5,25
y0 = 1,5^3-1,5*1,5+3 = 4,125
y - y0 = a(x-x0) > y-4,125 = 5,25(x-1,5)
y = 5,25x-,375

og beskriv løsningerne!
Bør jeg få 2? eller er det slet ikke det her der bliver spurgt om? For fandt lidt på studieportalen om at det skulle give -1 og +1 :(

Det er lidt forvirrende, når du skriver opgaver op... For når du skriver: f'(x)=1.5, så beskriver du hældningen af den oprindelige funktion på en måde, så du siger, at den er lineær (eksempelvis er den differentierede til tangensen fra den forrige opgave = 1.5)... Jeg er ret sikker på, at det ikke er det, du vil fortælle... ;-)

Du vil gerne finde tangenten til punktet (1.5;f(1.5)) for funktionen x^3-1.5x+3?

Det gætter jeg på, så det regner jeg videre med :)

f´(x)=3*x^2-1,5
tangent: Vi ved at x0 = 1.5, da (1.5,f(1.5))
a = f´(1.5) = 3*1.5^2-1,5 = 5,25
y0 = 1.5^3-1,5*1.5+3 = 4,125
y– y0 = a(x – x0) = y-4,125=5,25(x-1,5)
y = 5,25x-3,75

Så næsten det samme, vi får :)

Nej, tror faktisk ikke det er det jeg vil :-D

Opgaven lyder:

Løs ligningen f´(x) = 1,5 og gør rede for løsningernes betydning

Er det nu vi dimmitere? :)

Ahh...

Så det, du vil, er at du vil gerne finde ud af, hvor hældningen på den oprindelige graf er 1.5... Så var det rent faktisk rigtigt skrevet, men så er det det forkerte, vi er gået i gang med at regne :D

Du har funktionen: f(x) = x^3-1.5x+3
Vi har allerede differentieret den: f'(x) = 3x^2-1.5

Det, vi nu gerne vil finde er: f'(x) = 1.5

Så vi sætter ind:
1.5 = 3x^2-1.5

Det er en almindelig andengradsligning og ja, den giver 2 løsninger, nemlig x=1 og x=-1.

Det, du så skal beskrive er, hvad du har fundet frem til. Altså, hvad betyder det, at løsningerne er x=1 og x=-1...

Hmm, det svarer vel til at på x = -1 og x = 1 har vi en hældning på 1,5?

Ved ikke lige hvad jeg skal forklare - at den er positiv på hhv -1 og 1.

Det er de to punkter på grafen, hvor hældningen er 1.5, ja... og vel at mærke de eneste to steder (grafen er sådan en op-ned-op graf...)

Så i punkterne (-1;f(-1)) og (1;(f(1)) har grafen en hældning på 1.5, og dvs en tangent vil også have en hældning på 1.5 der... Det viser sig i den tidligere opgave, hvor vi netop fandt tangenten til (1;f(1))... Hvis vi finder tangenten til punktet (-1;f(-1)), så vil den ligeledes have en hældning på 1.5...

Har siddet og kigger på det med farverne du skrev tidligere.

3x^2-1,5

a=3
b=1,5
c=??

eller er det

f(x) = x^3-1,5x+3 jeg skal lege med?

a=1
b=1,5
c=3

Som heller ikke giver mening for mig..

C er vel 0, som zorro skriver går konstanterne væk ved diff. regning.

Jeg ved ikke, hvad det der a,b,c er... Er det noget til en formel?

(Jeg er ikke så god til at huske formler... Regner bare... :( )

Ktothep - tænkte det nok, turde ikke skrive 0 :o) Så forstår jeg det.

Zorro - yeps, den hedder d = b^2-4*a*c, men håber jeg engang får det lige så godt under huden som du har, synes det er spændende at least :)

Okay, forstår det stadig ikke.

d=b^2-4*a*c
d=-1,5^2-4*3*0 = -2,25.

Kan næsten regne ud at det skal være +1,5, men kan ikke lige se hvorfor det skulle give mening :S

Ahh... Til diskriminanten... Så er jeg med :)

Diskriminanten er til andengradsligningen... Dvs f'(x)

Så (-1.5)^2-0 = 2.25 (andet led er godt nok 4*3*0, men når man ganger med 0, så giver det 0)

EDIT: Indsat parentes, så det ikke forvirrer med fortegn :)

@kent

Minus opløftet i anden giver plus, så (-1,5)^2

Har siddet for længe med det tror jeg, kæft jeg er døsig.

Skal lige have det lort her færdigt.

3*x^2-1,5
d = b^2-4*a*c
d = 1,5^2-4*3*0 = 2,25
x = -b±√d/2a = -1,5±√2,25/2*3 = -1.5±1,5/6 =

Hvor går det nu galt? :)

ktothep - hmm, gør mine lommeregnere ikke automatisk?

Kan selvfølgelig godt se hvorfor though, tænker ikke lige så klart længere.

Husk at b er fundet til -1,5 så der står - (-1,5) :)

Og så mangler du teknisk set også nogle paranteser... Men hvis du bare regner det rigtigt, så er det jo "ligemeget" :)

x = -b±√d/2a = -(-1,5)±(√2,25)/(2*3) = (-(-1.5)±1,5)/6 =

Bedre med ()?

Hvordan dælen får jeg -(-1,5)+1,5 og -(-1,5)-1,5 til at give 6? :S Hvad gør man med dobbelt minusser :D

Som skrevet der bliver x = 0,5 og x = 0, må indrømme at jeg ikke har læst hele tråden igennem, så kan ikke lige gennemskue hvorfor du vil have resultatet til x = +-1 :)

Jeg vil have det til at give +-1, fordi det er samme opgave som -> www.studieportalen.dk/forums/Thread.aspx?id=1411087

Det du har skrevet svarer til at du isolerer x i :

ax^2 + bx + c = 0, husk at du har f'(x) = 1,5 og ikke f(x) = 0.

Så der må stå

3x^2-1,5 = 1,5 hvor du så kan udlede x og løse denne.

Virkelig lang tid siden jeg har gjort det her i hånden, på uni bruger vi lommeregner og programmer af gode grunde, så hæng mig ikke alt for meget op på det. Men sættes din f'(x) = 1,5 og løses på lommeregneren fås de ønskede x værdier :)


EDIT: kan se zorro allerede har skrevet noget lignende tidligere, så måske det ikke var der her dit spørgsmål gik på?

Prøvede lige på lommeregneren - der må stadig være noget jeg misser :)

f(x):=x^(3)-1.5*x+3 -> udført
(f(x),x) -> 3.*x^(2)-1.5
solve(f(x)=1.5,x) -> x=−1.5674683748524

Mon jeg bare skulle starte fra ny imorgen :)))

Du skal sætte f'(x) = 1,5 og ikke f(x) så burde det hjælpe :)

Jeg er slet ikke med på, hvad du nu prøver på :D

@zorro

Går ud fra han vil finde rødderne i f'(x) = 1,5.

At der så er kommet diskriminant og rødder ind, som gælder for andengradsligningen = 0, roder det lidt :)

Ahh...

Først kigger vi på ligningen:

1.5 = 3x^2-1.5

Den omskriver vi til noget, der passer til din formel (ax^2+bx+c = 0)

3x^2+0x-3 = 0

Så er a = 3, b = 0, c = -3

d = 0^2-4*3*(-3) = 36

Løsninger: -0+-(kvadratrod 36)/(2*3) = (0+-6)/6 = +1 og -1

zorro nailed it.

@kentkay

Husk på at de regneregler for diskriminant og rødderne kun gælder ved f(x) = 0 :)

Så du skulle bare huske, at din ligning skal være lig 0, før du begynder at regne med formlen... Så går det op :)

Men skulle den ikke være lig 1.5?

:))))))))))))))))))))))))))))

Som udgangspunkt jo, men for at benytte de Formler du gerne vil bruge, er du nødt til at isolere så du har et udtryk = 0 :)

Så som zorro skriver bliver f'(x) = 1,5 omskrevet så disse formler for diskriminanten og rødderne kan benyttes.

Det er den jo også...

Ligningen hedder: f'(x) = 3x^2-1.5

Hvis vi sætter den lig 1.5, så har vi: 1.5 = 3x^2-1.5

Så langt er vi enige?

--

Kan vi så også blive enige om, at:

1.5 = 3x^2-1.5 er det samme som 0 = 3x^2-3 ?

(Jeg har bare trukket 1.5 fra på begge sider af lighedstegnet)

Så det er det samme, og vi har stadig sat ligningen lig 1.5, men da du skal have 0 på det ene side for at kunne bruge din formel til at regne diskriminanten ud, så flytter vi lidt rundt på det først. Det er stadig den samme ligning :)

Håber det giver mening :)

Jep, forstod godt at vi samlede c og sådan :)

Tror det kommer til at kræve MEGET tid, vi er først lige begyndt i den her uge, mon ikke det kommer hvis jeg arbejder hårdt :)

Hvertfald SUPERFEDT!!! at i har taget jer tid til at hjælpe mig, er dybt taknemmelig :)

Og smider lige det sidste ind:

c) find f´(x) = 1,5 og redegør for løsningerne.
ax^2+bx+c = 0
1.5=3x^2+0x-1.5
3x^2+0x-3 = 0
d = 0^2-4*3*(-3) = 36^2
x = -b ± (√36)/2*a = -0±6/6 = x=1 v x=-1

Vi kan hermed konkludere at (-1;f(-1)) og (1;f(1)) har grafen en hældning på 1,5. Det bekræfter vores tidligere resultat også.

Så længe du gider sætte dig ind i det, så skal det nok komme... Det er den vigtigste forudsætning for at lære det... Og du virker ganske stædig mht at lære det, så det tror jeg bestemt nok, at du skal få styr på :)

Det lækkert lige at få fokus væk fra bridge design eksamen i morgen og genopfriske gymnasie tiden ;)

Men ja, du kan ligeså godt forberede dig på at det bliver meget værre end det her, men en rigtig god ting at lære så man har basis:)

Og lige en finurlig i din mellemregning...

d = 36... IKKE d = 36^2... men det mente du heller ikke ;-)

Haha :)

Er så smadret i hovedet - ville lige kigge på næste afleveringsopgave - finder så ud af at jeg har lavet den forkerte, og vi ikke havde lært alt det her endnu!! :))))

Haha... Det med at lave en forkert opgave har jeg gjort 3(!!) gange i det her semester... Jeg fatter virkelig ikke hvordan :D

Så du jo milevidt foran allerede! :D

Så er jeg på den igen, nu med optimering.

Jeg har både set min undervisers egne YT-videoer og Frividen.dk, men det er alligevel ikke rigtigt eksempler der passer på min problemstilling. Måske fordi det stadig gør mig forvirret :)

Kassen er 2,4m^3.
Kassen er 0,5m høj.
Kassens længde har y og bredden x

Først skal jeg opstille en model for T(x)

T = x • y + x • y + x • d + x • d + y • d + y • d
T = 2x•y+2x•d+2y•d

Så får jeg afvide at x = 2,19089 og at jeg skal finde den minimale T(x) i forhold til rumfanget.

Okay, super.

Rumfanget kendes ved V = y*x*d -> 2,4 = y*2,19089*0,5
2,4 = 2,19089•y•0,5
Y = 2,19089•0,5/2,4
Y = 0,456

Er der nogen der gider at bruge lidt tid på, hvad eg specifikt gør forkert? Jeg kan jo godt regne ud at længden ikke kun er 0,456, men hvorfor jeg fejler, kan jeg ikke rigtigt forstå.

Du får løst den sidste ligning forkert - y bliver ikke isoleret korrekt.

Måske er det bedre, hvis du kan uploade hele opgaven. Opgaveformuleringen ser forkert ud, som den står der.

Hva er T(X)? Overfladeareal?

Får du virkelig at vide at x = 2,19089? Altså med 5 decimaler?

Enig med henry - uploade hele opgaven.

Prøv og tjek din isolering i V formlen igen :)

Kan sgu godt se den isolering sejler lidt, men uploader lige det hele.

Sådan her lyder hele opgaven:
"3.1 OptimeringPetersen er ved at lave en 2,4m3faskinetil regnvand. Han skal håndgrave hullet, men hans spade kan kun stikke 0,5 m ned i jorden (hvilket derved bliver faskinens dybde, d). Faskinen fyldes med sten og pakkes ind i fiberdug. Faskinens bredde benævnes xog længden, y.a) Modellering. Opstil en model for faskinens overfladeareal, T(x).b) Vis at når x= 2,19089 haves et minimalt overfladeareal T(x)i forhold til rumfanget"

Ok, nu ligner det en optimeringsopgave igen :)

Opgaven består som altid af 2 led.

a) Først skal man opstille en funktion, her T(x). Det går ud på at eliminere alle de andre variable, her y og d, så man kun har en funktion af x tilbage.

b) Her skal man finde x, så T(x) bliver mindst mulig. Svaret er så givet i opgaven, så man skal "bare" vise beregningerne frem til. Som altid i optimeringsopgaver skal man differentiere den funtion man fandt i (a) og sætte lig 0.

Så min fel foregår allerede, da jeg ikke formår at ændre y, det havde jeg lidt på fornemmelsen, da jeg tog mig selv i ikke at kunne stå ved udelukkende x'er.

Men hvordan gør jeg det?
I alle mine tidligere eksempler + dem jeg finder på nettet, er jeg ikke stødt på denne type. Enten er l og b = x eller også er b = x og l = 2-x or so.

Jeg er ikke stødt på et nøgent Y før, og har svært ved lige at komme videre :)

Til a) skal du bruge følgende oplysninger:

d = 0,5
V = x*y*d = 2,4
T = 2*x*y + 2*x*d + 2*y*d (som du også selv skrev)

Du skal have eliminere y og d i den nederste ligning, så du får T(x) = [et udtryk med kun x som variabel].

d er hurtig at eliminere, for d = 0,5

y eliminerer du ved hjælp af ligningen V=xyd som kan omskrives til y = V/xd. Her kender du V og d, så du får y = tal/x. Det sætter du ind i ligningen T(x)= ...

Ser nu, at der kan være tvivl om opgavens formulering. "Faskinens overfladeareal"? Er det den del, der vender opad, eller er det det samlede overfaldeareal på alle faskinens 6 sider?

Anyways vil det give det samme i sidste ende. Alt det regneri i øvrigt bare for at nå frem til det indlysende resultat til sidst, at man optimerer faskinens rumfang ved at gøre den kvadratisk :)

Jeg har lidt problemer her.

Jævnfør:
y2 = c-(b^2-1)/(4*a)
ved f(x) = x2 - 4x + 3
3-(-4^2-1)/(4*1) = 0,75

Men jeg kan ikke få 3-(-4^2-1)/(4*1) til at give 0,75, men derimod 1,25-

Mht. den sidste tror jeg du skal løse den sådan her.

Du skal vise at x=2,19 minimerer forholdet mellem overfladearealet og rumfanget, kald den funktion for f(x,y,d)

f(x,y,d) = T(x,y,d)/V(x,y,d) = (2xy + 2xd + 2yd) / xyd = 2(1/d) + 2(1/y) + 2(1/x)

Du ved at xyd = 2,4 og d = 0,5 <=> xy = 4,8 <=> x = 4,8/y

Sæt det ind i f og du får en funktion i y, der hedder:

f(y) = 2(1/d) + y(1/2,4) + 2(1/y)

Differentier nu og sæt lig med 0:

f'(y) = 0 <=> 1/2,4 - 2(1/y^2) = 0 <=> 1/4,8 = 1/y^2 <=> 4,8 = y^2 <=> y = 4,8^(1/2) = 2,19

Så tror jeg bare du mangler at se på monotoniforholdene for f(y) så er du i mål ...

/rickrick

Stod helt af der.

Parablens brændpunkt (x ; y) kan beregnes med formlen: (x2 ; y2) = (-b/2*a ; c-(b^2-1/4*1))

a) Vis at grafen til andengradspolynomiet : f(x) = x2 - 4x + 3 har brændpunkt i (x2 ; y2) = (2 ; -0,75)

Sådan lyder hele opgaven - den burde være ret ligetil, men det er den åbenlyst ikke for mig.

Hvor får du 2,19 fra? Er det en generel regel, jeg ikke er blevet introduceret for?
Kan generelt ikke rigtigt få ovenstående til at give sammenhæng med min opgave overhovedet.

:-(

Mit svar var til dit #99, hvor du skriver

"... Vis at når x= 2,19089 haves et minimalt overfladeareal T(x)i forhold til rumfanget"

Og det viser du ved ovenstående :-)

Er jeg gået glip af noget?

Nej, jeg er bare kommet videre - opdaterer i tråden, når jeg har problemer, derfor det er lidt rodet.
Men jeg har styr på det nu, jeg skal bare lære at tage en pause når jeg har siddet med det for længe, og lige tage lidt tid fra det, så jeg ikke stirrer mig blind :)

Men tak for hjælpen anyways, virkelig fedt at randoms gider hjælpe, når man er i problemer! :)

Mht. din #108

Du har en funktion af formen ax^2 + bx + c

Hvor a=1, b=-4, c=3

Så får du brændpunkt:

x = -(-4)/2 = 2

y = 3 - ((-4)^2 -1 / 4) = 3 - (16-1)/4 = 3 - 15/4 = -0,75

Jeg tror i din formel, at det skal være b^2-1 divideret med 4 :-)

Du har helt ret - det kom jeg også frem til, men min lommeregner drillede og jeg glemte lige folkeskolereglen at - og - giver + :o)

He he - ja det kan jo smutte.:-)

Er nysgerrighed. I hvilken forbindelse sidder du og roder med det her matematik?

Matematik b, fjernundervisning :)

Så den kontakt jeg har med min underviser foregår over mail, og det kan godt tage et par dage at få et svar.

Ahh ok, bare smid noget mere op hvis det er - altid hyggeligt med nogle "gode gamle opgaver" - bedre end at sidde og glo ind i fjernsynet.

Har siddet med det siden kl 4, men du kan være sikker på at jeg bumper tråden næste gang jeg er landet i uføre ;)

Thanks once again :)

Har lige en mere.

Jeg forsøger at finde nulpunktet, når x = 0

f(x) = x^2-4x-4
d = b^2-4*a*c = -4^a-4*1*-4 = 16-16 = 0
x = -(-4) ±√0/2*1 = 2

Men hvis jeg skriver solve(x^2-4x-4=0,x) giver den mig x=−2*(√(2)-1) or x=2*(√(2)+1)

d = b^2-4*a*c = -4^2-4*1*-4 = 16+16 = 32

FUCKING -- shit.

Anden gang på 2 dage.

Thanks man :)

Kan jeg godt bare angive x=−2*(√(2)-1) or x=2*(√(2)+1) som TI siger, eller skal jeg angive det som (4+√(32))/2 = 4,83 or (4-√(32))/2 = -0,83

Hvis nederste - hvorfor skriver TI ikke det?

Virkelig lang tid siden jeg har brugt min TI-89 (ved ikke hvilken TI du har), men grunden til at din TI ikke angiver det i decimal-tal kan skyldes at du har sat den til at vise det eksakte resultat.

Jeg kunne i hvert fald selv bestemme om den skulle vise eksakt resultat, eller decimal-tal samt antallet af decimaler jeg ønskede.

Hmm - okay, tak. Det vil jeg kigge på.

Jeg bruger TI-Nspire (Computerlommeregner).

Se evt her side 16 for mere info:

education.ti.com/sites/UK/downloads/pdf/First_Steps_with_TI-Nspire_CX.pdf

Custom + enter på en TI89 for at få det i decimal tal.

Måske noget lignede på computeren.

Og hvordan det skal angives. Er det den færdige løsning ville jeg bruge decimal tallet, er det ikke den færdige løsning ville jeg bruge det først skrevet som TI siger :)

Hvorfor giver

- Konstanten forsvinder og så differentierer vi -e^-x, som giver -e^-x*(-1) = e^-x

Hvad spørger du om?

kentkay skrev:
Hvorfor giver

- Konstanten forsvinder og så differentierer vi -e^-x, som giver -e^-x*(-1) = e^-x

Thanks man :)

Må jeg spørger hvad du studerer/arbejder med?

Jeg studerer HA jur... Skal til at i gang med 2.semester... Vi skal faktisk ikke have matematik mere, så nu skal du ikke lave det alt for indviklet i fremtiden ;-)

Hej igen :-),

Virker måske lidt nollert, men har brug for hjælp til en opgave, til trods for at svaret står længere oppe.

Sådan her lyder hele opgaven:
"3.1 OptimeringPetersen er ved at lave en 2,4m3faskinetil regnvand. Han skal håndgrave hullet, men hans spade kan kun stikke 0,5 m ned i jorden (hvilket derved bliver faskinens dybde, d). Faskinen fyldes med sten og pakkes ind i fiberdug. Faskinens bredde benævnes xog længden, y.a) Modellering. Opstil en model for faskinens overfladeareal, T(x).b) Vis at når x= 2,19089 haves et minimalt overfladeareal T(x)i forhold til rumfanget"

Første besvarelse:
Side 1 (den side der ligger tættest på x) = x•d
Side 2 (den side der ligger tættest på y) = y•d
Side 3 (den øverste side) = x•d
Side 4 (den modsatte side af side 1) = x•d
Side 5 (Den modsatte side af side 2) = y•d
Side 6 (den modsatte side af side 3) = y•x

T= x•d + y•d + x•d + x•d + y•d + x•d

T=xd^2+yd^2+xy^2
For at finde T(x) må ligningen kun indeholde tal og x. Vi skal derfor omskrive ligningen.

Vi kender at d = 0,5
V=x• y•d
2,4=x•y•0,5
y=2,4/(x•0,5)
y=4,8/x

T(x)=0,5x^2+〖(4,8/x)^2〗^ +〖2,4〗^2

Anden del:
2) Vis at når x = 2,19089 haves et minimalt overfladeareal T(x) i forhold til rumfanget

Jeg kan sagtens se at svaret står udpenslet ovenover, men det er ikke den måde vi har lært det på - tror jeg. :)

Nedenstående er jo åbenlyst ikke korrekt, men hvor sker fejlen?

Fejlen ligger i at du ikke løser opgaven :-)

Du bliver spurgt om ved hvilket x at T(x) er minimalt i forhold til rumfanget. Dvs. den ligning som du skal differentiere er T(x)/V(x), hvor V(x) er dit rumfang givet ved V(x)=x•y•d. Indsæt din kendte y=4.8/x samt dit d=0.5. Så har du så et udtryk for T(x)/V(x) som du kan differentiere, sætte lig 0 og løse for x.

Det som du har gjort er bare at finde den minimale overfladeareal for alle rumfang.