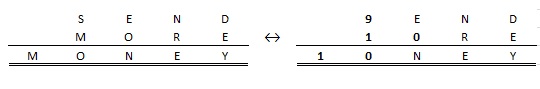Er du frisk på en lille tal-opgave? (nu med hint)

Hey guys

En lille tal-opgave, se om I kan løse den. Lad vær med at skrive løsningen hvis du finder ud af det.

Here it goes:
SEND+MORE=MONEY
Dette regnestykke har én løsning. Man må kun bruge værdierne 0-9 og to forskellige bogstaver må ikke have samme værdi og bogstaver der er ens er/skal være samme værdi.

Eks. S er 5, så må ingen andre bogstaver være 5. M er 6, så er M i "More" og "Money" værdien 6.

Enjoy :)

// KD

EDIT: Hvis en admin lige gider flytte topic til "off-topic" tak :)
EDIT: M må ik være 0 (giver lidt sig selv ville jeg mene men nu det sagt)

Den har da flere løsninger end én?

Hvis man starter rigtigt, er den ikke så svær :)

Og to løsninger har jeg svært ved at se...?

@ Nilsson
Jeg kan ik se to løsningen men dem ka du evt poste engang i aften :)

@ Zorro
Korrekt

Fik da helt lyst til lidt matematik... Men forstår ikke helt opgaven.

SEND

S=1
E=2
N=3
D=4

Er SEND så = 24, 10 eller 1234?

MVH Skod

@skod

Det er et plusstykke...

Ligesom hvis der havde stået:

937+518 = 1455

Tallene er bare byttet ud med bogstaver og så skal du finde ud af, hvilke bogstaver, der er hvilke tal... Og hvert tal må kun være ét bogstav og omvendt.

Så i dit eksempel er SEND = 1234

SEND+MORE=MONEY

3456+7894=78542

Regnestykket passe så bare ikke. Men E er 4 her, M er 7, O er 8

Ok. fair nok. Dengang jeg gik i skole ville regnestykket betyde S*E*N*D+M*O*R*E=M*O*N*E*Y

Den kan i jo så se om kan regnes ud, hvis i er færdige med den første ;)

@skod

Den har jeg klaret...

E = 0

Resten er ligegyldigt ;)

haha. true. Så prøv at løse den med 1-9.

Haha, jeg havde også misforstået det kan jeg så se.

Og når I bliver færdige, kan I jo fortsætte med USSR+USA=PEACE

Jeg giver op. Tømmermændende vandt.

Damn jeg var tæt på
9365 + 1273 = 12638

Problemet er dog at det kun giver 10638

Back to square one

Ohep1 skrev:
Og når I bliver færdige, kan I jo fortsætte med USSR+USA=PEACE

Plz..ikke flere opgaver i dag.

Min enlige hjernecelle kom på overarbejde ved løsningen af den første opgave.

Jeg ved det, jeg ved det. Hvad har jeg vundet?

Adagio skrev:
Jeg ved det, jeg ved det. Hvad har jeg vundet?

Mon ikke vi alle får en keramikugle ?

Ohep1 skrev:
Og når I bliver færdige, kan I jo fortsætte med USSR+USA=PEACE

Den er lettere end den oprindelige.

skal folk have hjælp? Kan give et hint hvis I ik selv har fanget det der er "åbenlyst".

Ved simpel analyse fåes:
- To tal som 4 cifre lægges sammen og giver et tal på 5 cifre. Det betyder at begge tal max er 9.999 og summen derfor ikke kommer over 20.000. Ergo skal første tal (M) i summen være 1. Når M er 1, så er MORE max 1999, hvilket gør at SEND skal være minimum 8001.

Derfra har jeg ikke lige nemt kunne analysere videre

@Razga

Medmindre M er 0...

Jeg fandt dog en løsning med M=1.

Derefter kan O regnes ud.
Derefter kan nogle egenskaber ved forskellen på E og N regnes ud.
Derefter kan S regnes ud.

Derfra endte jeg med at prøve mig frem... lidt usselt...

Må også nok indrømme, at jeg kun analyserede mig frem til de første stykker... Og derefter havde en ide om, hvilke af de resterende, der var et stort og et lille tal... hvorefter jeg bare prøvede de sidste muligheder... Jeg tvivler dog også på, at man kan analysere sig frem til det hele uden at tage en chance undervejs (men kan selvf tage fejl - så grundig har jeg heller ikke været :) ).

Ret tæt på, hvad drhoho gjorde, tror jeg... Man kan jo godt komme med kvalificerede gæt og ikke bare randomly prøve sig frem... Men ved ikke, om det er snyd... :)

Selvfølgelig er det noget med at prøve sig frem.

Men nogle af bogstaverne ligger rimelig hurtig fast.

For mit vedkommende var det bogstaverne M, O, S og R.

Dernæst forskellen/differencen mellem E og N.

Fin lille opgave :)

Har skrevet et hint til løsningen med gennemsigtig til dem der er gået døde

Bogstaverne M O S R kan i den rækkefølge regnes ud ved at konkludere på det foregående tal.

Dernæst skal forskellen/differencen mellem e og n findes.

Det sidste step ligger i at D+E=Y+10

Dette er de hint jeg giver.

Jeg søgte bare på nettet :-)

Det der er åbentlyst er at M skal være 1 (må ik være 0, giver jo ingen mening). Er M 1 skal S være 8 eller 9. men da M = 1+9/8og en mente = 0 gør det at O=0 og derfor ka der ingen mente være og derved S=9.

-KD- skrev:
Det der er åbentlyst er at M skal være 1 (må ik være 0, giver jo ingen mening). Er M 1 skal S være 8 eller 9. men da M = 1+9/8og en mente = 0 gør det at O=0 og derfor ka der ingen mente være og derved S=9.

Øh... hvor finder du den forudsætning at M ikke må være nul? Man kan da altid sætte alle de nuller foran et et tal man vil, uden at ændre ved dets mening. Det er blot ikke almindeligt at bruge det.

Men godtaget at M ikke er 0, så følger åbenlyst at M er 1, da XXXX+XXXX<2XXXX altid.

Tilsvarende følger nu O=0, da XXXX+1XXX<12XX altid, og 1-tallet allerede er brugt.

Vi har nu SEND + 10RE = 10NEY

Det betyder for hundrederne at E+0(+evt. mente) = N. Da E og N ikke må være samme tal betyder det at der skal være en mente, og N = E+1. Det medfører også at E ikke kan være 9, da N ikke må være 10 (ikke et enkeltciffer).

Lad os se på S. For at få summen op over 1000, er det klart enten har vi SEND = 9XXX eller SEND = 89XX. Men da E ikke må være 9, kan S kun være 9.

Det giver så 9END + 10RE = 10NEY.

Herfra gættede jeg blot på forskellig værdier af E, indsatte E og N=E+1, og puslede mig frem.

Tror det her er rigtig:

9567 SEND
1085 MORE
10652 MONEY

@drhoho
Korrekt, burde jeg skrive i reglerne. Men pointen er at det er et fuldt ud regnestykke og du ser aldrig et regnestykke hedde 0985+00573 vel?

easy money.. 2 min og done :-)

løste jeg da jeg gik i 3. klasse så mon ikke alle kan løse den.

Jeg kom også relativt let frem til:
M=1
o=0
N= E+1

Men hvordan man skulle komme videre derfra fandt jeg aldrig ud af (jeg gad ikke prøve mig frem)

Men er der er enreel matematisk løsning, eller er det bare en logik/trial and error opgave? For så føler jeg mig sgu snydt! :D

Så fandt jeg vist endelig løsningen uden at prøve mig alt for meget frem. Det er svært at forklare, men jeg prøver:



Som forklaret af de andre har vi nu M=1, O=0, N=E+1 og S=9.

For overskuelighedens skyld forkorter jeg stykket til END + RE = NEY

Da N = E + 1 vil regnestykket komme til at ud som 56D+RE=65Y, 45D+RE=54Y eller 34D+RE=43Y osv. Humlen er her at tallet RE nødvendigvis skal være 80+. Da 9 er optaget må R=8.

Dette medfører også at D+E>9 da vi skal bruge en i mente fra enerne. Da Y ikke kan være 0 eller 1, kan vi indsnævre mere og sige D+E = mindst 12.

På nuværende tidspunkt kan vi se da N højest kan være 7 (8-9-10 er optaget), kan E højest være 6. Hvis N=7 og E=6, kan vi ikke give D en værdi så D+E bliver mindst 12. Hvis vi sætter E=4 kan vi heller ikke vælge høj nok værdi til D til at opfylde D+E=mindst 12. Den eneste mulighed for at opnå dette er hvis E=5 og D=7.

Hvis E=5 så er N=6

Vi har nu fundet følgende:

9567+1085=10652

Som ud fra mine beregninger er den eneste mulige løsning.

Fik også lige lavet USSR+USA=PEACE. Her er en kort forklaring, hvis der er nogen der er interesserede. Den er en del nemmere når man lige har lavet den første da de har en del til fælles:


P=1 og E=0 da 9999+999=10998, så PEACE<10998.

U=9 da 8999+899=9898<10xxx

Nu har vi så:

9 S S R
+ 9 S A
=1 0 A C 0

S=A+1, da vi har et 9 tal på 100ernes plads. Dette betyder også at der ikke må komme nogle "i mente" fra 10erne, så 2 x S < 10.

Da 1 er optaget og S=A+1, kan S kun være 3 eller 4.

Da der er et 0 på enernes plads i resultatet må der nødvendig blive overført 1 i mente til 10erne. Det betyder at C=S+S+1. S kan således ikke være 4 fordi 4+4+1=9 er optaget, så derfor er S nødvendigvis = 3.

Da S=3 må C være = 3+3+1=7 og A=3-1=2

Tilbage er kun 8, som så må være = 8 for at få stykket til at gå op:

9338+932=10270

Der står intet? men det måske joken?

Gennemsigtig skrift, marker området for at se løsning :)

Skreiber er spot on :) Så kan folk selv se svaret hvis de vil :)

5 liniers programkode, så har man svaret :-) Der er i øvrigt 24 løsninger når M=0 og kun 1 når M=1.

SteenV skrev:
5 liniers programkode, så har man svaret :-) Der er i øvrigt 24 løsninger når M=0 og kun 1 når M=1.

24...?!?

Det lyder vildt (uden at jeg har checket efter). Tallene må kun bruges én gang hver?

9567 + 1085 = 10652

@Zorro

Der også 9! / 2 = 181440 forskellige assignments hvis vi kræver at M = 0.

S = 2, E = 8, N = 1, D = 7, M = 0, O = 3, R = 6, Y = 5
S = 2, E = 8, N = 1, D = 9, M = 0, O = 3, R = 6, Y = 7
S = 3, E = 7, N = 1, D = 2, M = 0, O = 4, R = 6, Y = 9
S = 3, E = 7, N = 1, D = 9, M = 0, O = 4, R = 5, Y = 6
S = 3, E = 8, N = 2, D = 1, M = 0, O = 4, R = 6, Y = 9
S = 3, E = 8, N = 2, D = 9, M = 0, O = 4, R = 5, Y = 7
S = 5, E = 7, N = 3, D = 1, M = 0, O = 6, R = 4, Y = 8
S = 5, E = 7, N = 3, D = 2, M = 0, O = 6, R = 4, Y = 9
S = 5, E = 8, N = 4, D = 9, M = 0, O = 6, R = 3, Y = 7
S = 6, E = 4, N = 1, D = 5, M = 0, O = 7, R = 3, Y = 9
S = 6, E = 4, N = 1, D = 9, M = 0, O = 7, R = 2, Y = 3
S = 6, E = 5, N = 2, D = 4, M = 0, O = 7, R = 3, Y = 9
S = 6, E = 8, N = 5, D = 1, M = 0, O = 7, R = 3, Y = 9
S = 6, E = 8, N = 5, D = 3, M = 0, O = 7, R = 2, Y = 1
S = 7, E = 3, N = 1, D = 6, M = 0, O = 8, R = 2, Y = 9
S = 7, E = 4, N = 2, D = 9, M = 0, O = 8, R = 1, Y = 3
S = 7, E = 5, N = 3, D = 1, M = 0, O = 8, R = 2, Y = 6
S = 7, E = 5, N = 3, D = 4, M = 0, O = 8, R = 2, Y = 9
S = 7, E = 5, N = 3, D = 9, M = 0, O = 8, R = 1, Y = 4
S = 7, E = 6, N = 4, D = 3, M = 0, O = 8, R = 2, Y = 9
S = 7, E = 6, N = 4, D = 9, M = 0, O = 8, R = 1, Y = 5
S = 8, E = 3, N = 2, D = 4, M = 0, O = 9, R = 1, Y = 7
S = 8, E = 4, N = 3, D = 2, M = 0, O = 9, R = 1, Y = 6
S = 8, E = 5, N = 4, D = 2, M = 0, O = 9, R = 1, Y = 7
X = 24

ok

Zorro, lol :)

Hvordan laver man det der usynlig skrift?





edit, dohhh.... mer lol