Expiring make-up cash game staking a´la Sauce123

Hey Pokernet,

Her er en for the math whizzes.

Er der nogen der er så skarpe at de hurtigt kan give mig gode pointers om hvordan Sauce ved hjælpe af bla std dev og winrate, regner længde på intervaller og profit splits ud på de staking deals han tilbyder på saucestakes.com?

Sagen er at jeg i lang tid har haft fyr på en, for ham, lidt for saftig deal, og nu vil jeg gerne give ham en ny mere fair deal for alle.

Alle matematik kompetente input er mere end velkomne.

/Mark P

på slide 10 kan du se hvordan man udregner konfidensintervaller:
www.math.ku.dk/~helle/StatBK/08-09/slides/handout2-2.pdf

U er din nuværende winrate, og det der pudsige O med stregen på toppen er std.dev.

De 1,96 han ganger ind på, fortæller om at hans interval er betegnes med 95% sikkerhed. Du kan prøve at lege med 1,64 som er værdien for et 90% konfidensinterval. Dette vil gøre intervallet lidt mindre.
Men handler det ikke bare om at du skal presse ham ned i %'er?

Jeg gætter på at Sauce også bruger et 95%-interval, da jo højere intervallet er, desto mere udligner det den varians han skal tage højde for.

Jo han skal helt sikkert presses ned i %'er. Spørgsmålet er hvor meget. Jeg vil gerne have nogle tal på hvad der kunne lyde rimeligt. Det lyder godt det du har fundet. Kigger på det efter session. Tak for hjælpen.

Jeg tror at hvis du skal have rigtig hjælp, så skal du fremlægge nogle tal, men det ved jeg ikke hvor interesseret du er i.

Sorry for OT

J_Knish
Er du tilbage på pokerscenen? Hvad har du lavet de sidste 4 år? :)

De beregner ikke "længder" af intervaller - dem kan man selv vælge. Pointen er, at de itererer stakingen efter hvert interval, så de æder et givent tab i et interval, og derefter resetter dealen til det næste interval. Det gør, at de bliver nødt til at vurdere sandsynligheden for antal "losing intervals".

Sandsynligheden for et losing interval kan beregnes på baggrund af en antaget winrate og SD. Jo højere winrate og jo lavere SD, jo færre losing intervals, og følgelig bedre deal for stakeren.

Deres målsætning er givetvis at have en gennemsnitlig deal på 50/50, men for at kunne det, samtidig med at variere intervaller (dvs. ikke have en fast mand på en stake, som du beskriver, men tage folk ind for e.g. 3x50k hands), skal de have en model, der beregner sandsynligheden for antal tabende perioder.

Det avancerede for deres model er at konstruere den, således at de opnår 50/50 på hele deres stakinghold, som består af en række forskellige intervaller igang samtidig. Dertil skal de også vurdere sandsynligheden for "continuation" (stakeren sagde oprindeligt ja til 2 intervaller, men sandsynligvis er han mere klar på 5 - ish). Det er dog ret simpelt at lave modellen for én stakingaftale, og kan gøres i Excel, med lidt simpelt kendskab til statistik.

@Hermod og Asger

Tak for svarene. Det lyder som om det er noget i har styr på. Beklager min formulering Asger, jeg er godt klar over at det netop er sådan deals'ene på saucestaking bliver skruet sammen. Sagen er at ham jeg staker har brug for forholdsvis korte intervaller da han skal bruge penge til jævnlige faste udgifter.

Han og jeg skal så have kigget igennem hvad hans gennemsnitlige volumen er og ramme noget der ligner månedsintervaller on average og så finde ud af hvad en fornuftig profit split hedder for et sådant interval. Jeg har faktisk ikke noget imod at fremlægge tal så når jeg får noget fra ham poster jeg igen.

@MoPe

Jeg har som sådan aldrig forladt pokerscenen :) Har spillet poker på fuld tid de sidste fire år, men har bevidst skruet ned for den offentlige profil, da jeg ikke rigtig får nogen lir på at være skærmtrold. Desuden er det begrænset hvor interessant mit pokerliv er, da jeg efterhånden er nede på at spille 1-2 pokerturneringer om året. Cash game ftw :)

Ok, det tog sin tid. Har endelig været inde og rode lidt i min hests DB.

Han spiller FLHE

Med en winrate på 1,02 BB/100 (ja det er den oldschool big bets vi snakker om) og en standard deviation på 20,8 BB/100, er der så en af jer der kan give mig et godt bud på hvad split'en kunne hedde ved 10k hænder, 20k hænder og 30k hænder?

Bedste hilsner,

Mark P

Okay, hermed mit forslag.
Jeg kunne ikke få Monte Carlo simuleringen til at virke i Excel, så jeg har lavet en Matlab kode til formålet (indsat nederst)
Fra fordelingen fås et gennemsnit på 103.6 (BB/100) med en std. Afvigelse på 208.8 (BB/100) for 10K hænder. Som det ses af følgende histogram, ser fordelingen (heldigvis) ret normaltfordelt ud, så vi kan behandle det som en sådan fordeling.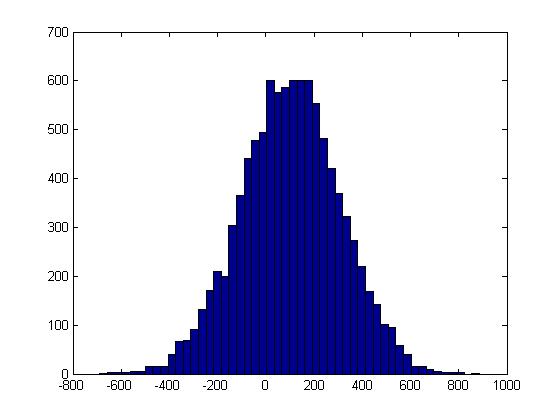



Herefter skal der formuleres en nøgle, der fordeler overskuddet 50/50 over tid, hvor alle negative events bliver sat til 0 (reset).Således har jeg opdelt data-settet i negative og positive events, fundet begges average, og fordelingen kan betragtes som en almindelig equity-beregning.

Notation:
P(x) = Sandsynligheden for x
Idét målsætningen er at fordele win ligeligt, skal stakees cut være:
AVG/2 = P(loss)*Neg_size + Cut*P(win)*Pos_size

Resultater:

For 10K hænder: 64.7%
For 20K hænder: 60%
For 30K hænder: 58%

Andre forslag til fremgangsmetode er velkomne.

==

clear,clc

WinDisp = zeros(10000,1);

for i = 1:10000

H = rand(100,1);
WR = 1.02;
SD = 20.8;

WinTrial = norminv(H,WR,SD);
Win_10K_Trial = sum(WinTrial);

WinDisp(i)=Win_10K_Trial;

end

hist(WinDisp,50)
AVG = mean(WinDisp)
SD_10K = std(WinDisp)

P_loss = normcdf(0,AVG,SD_10K)
P_win = 1-P_loss


Loss = WinDisp;

for i = 1:numel(Loss)
if Loss(i) < -400
Loss(i)=0;
end
if Loss(i)>0
Loss(i)=0;
end
end

Neg_size=mean(Loss)
Win = WinDisp;

for i = 1:numel(Win)

if Win(i)<0
Win(i)=0;
end
end

Pos_size=mean(Win)

Cut = (AVG/2-Neg_size*P_loss)/(P_win*Pos_size)

Føler min 20 år gamle matematiske studenterhue ikke rækker her ;)

Ret beset ved vi ikke om hestens resultater er normalfordelte. Ja, din graf er flot normalfordelt, men du bruger jo en normalfordelt funktion i dit program.

Beregningen kan sagtens ske at være brugbar, men det kan også vise sig at være forkert

Altså den normalfordeling bruger jeg til at undgå at sidde og sample på antal events i min trial-matrix (altså til at kunne formulere P_loss = normcdf(0,AVG,SD_10K). Det er primært fordi jeg ikke er så skrap til tælle-funktioner i Matlab.

Men derudover har du naturligvis i nogen grad ret. Vi skal dog huske på, at der i en 10K sample er 100 undersamples (tilsv. 200 for 20K) med en "global" StdDev (approksimeret fra en stor database). Det er så vidt jeg ved derfor en meget rimelig antagelse at forvente, at 10K samplen er normalfordelt, men jeg har kun taget det fra en lidt tilfældig hukommelse.

Altså, selv hvis jeg har 100 næsten fordelte undersamples, vil jeg stadig få en normalfordelt 10K sample - ish. Er det ikke noget i den dur?

Jeg kan ikke helt gennemskue incitamentet bag Sauces model frem for den "almindelige" model? Over tid (intervaller) og antal heste må splittet være det samme, såfremt modellen er korrekt. Hvad overser jeg?

NickHalden skrev:
Jeg kan ikke helt gennemskue incitamentet bag Sauces model frem for den "almindelige" model? Over tid (intervaller) og antal heste må splittet være det samme, såfremt modellen er korrekt. Hvad overser jeg?

Incitamentet er vel, at det er mere attraktivt for hestene (og derfor kan man få bedre og mere "motiverede" heste - der spiller bedre og vinder mere). Et mere kontinuerligt indgående cashflow er med til at sørge for, at hestene ikke mister motivation og fokus.

Hvorfor er det mere attraktivt for hestene, når splittet over tid (intervaller) må konvergere mod samme split%, hvad enten det er EV-split eller split i absolutte værdier? Variansen mindskes for stakees på kort sigt, men de får jo bare det mindre i afkast?

Pointen er, at de ikke risikerer at ryge i make-up, hvilket kan være en opslidende affære for alle parter. Samtidig giver det muligheden for, som i J_Knish's tilfælde, at udbetale månedlig løn.

Jeg tror de fleste (inkl undertegnede) ville kaste sig over en normalfordeling.

Det var mest denne jeg studsede over:

Som det ses af følgende histogram, ser fordelingen (heldigvis) ret normaltfordelt ud, så vi kan behandle det som en sådan fordeling.

Ja helt klart, det skulle jeg måske have forklaret lidt bedre.

Fedt Asger, tak!

Jeg er ret overrasket over at stakee's cut ikke skal være højere over så lille en sample som 10k hænder. Eller sagt med andre ord, forskellen mellem et 10k hænder interval og et 30k hænders interval (64,7 vs 58%) ikke er større. Sådan rent intuitivt føler du så at tallene er gode/nøjagtige?

Hvis du gør så satser jeg bare på at bruge dem.

Bedste hilsner,

Mark P

Hm, hvis jeg kigger på den her graf: www.pokerstrategy.com/forum/thread.php?threadid=37634 (den første af dem), så synes jeg også, at der burde være en større forskel mellem de to intervaller, men umiddelbart stemmer tallene.

Jeg kan lige poste de forskellige resultater, så man kan få lidt intuition for sandsynlighederne:

==================================================================================
10K:

AVG = 104.0600
SD_10K =206.9920
P_loss =0.3076
P_win =0.6924
Neg_size = -40.7063
Pos_size = 144.7663
Cut = 0.6440

==================================================================================
20K:
AVG = 213.8255
SD_10K = 293.0244
P_loss = 0.2328
P_win = 0.7672
Neg_size = -39.8591
Pos_size = 253.6846
Cut = 0.5970

==================================================================================
30K:
AVG = 326.2592
SD_10K =360.4024
P_loss =0.1827
P_win = 0.8173
Neg_size = -35.3975
Pos_size = 361.6567
Cut = 0.5737

==================================================================================

Noget af det jeg overvejede var, om jeg skulle lave et andet type af gennemsnit (for størrelsen af positive/negative gevinster), men umiddelbart mener jeg, at det burde passe.

Jeg har gen-overvejet cut-formlen. Den passer da, gør den ikke?

Men altså, sådan rent intuitions-mæssigt, så kan man jo se på graferne, at "jo større" win er (dvs. flere antal hænder), jo større er 95% intervallet også (nominelt). Ergo, så skal man op på et temmeligt stort antal hænder, før man nærmer sig 50%-fraktilen.

Men igen - det er et spørgsmål, om man vil omfordele profitten ligeligt mellem de to parter. Principielt kunne man jo sagtens nøjes med 20%, hvis man havde at gøre med en stensikker vinder, der var villig til at spille et stort antal hænder.

Hvis man fx staker 1000BB, og vedkommende indvilger i at spille 30K hænder/mdr, med en forventet winrate på 1 BB/100, så forrenter man sin investering med 15% månedligt, eller 180% årligt (hvis man ikke skifter takst). Jeg aner ikke, hvordan man sammenligner risikoen hér ifht. andre mulige investeringer, men vi skal op i nogle pænt risikable futures, før man møder den slags afkast.

"Say our hypothetical player was playing .50c/$1 6max nlhe. With a winrate of 10bb/100, over a sample of 10k hands, this player's expected win is .1 bb/hand * 10,000 hands= 1000bb, or $1000. To split that expected $1000 win 50/50 between player and backer, backer must collect more than 50% on winning 10k intervals to offset the losing 10k intervals in which he takes all of the losses. Taking 56.23% of winning intervals accomplishes this goal".

Sammenlignet med de tal der, så ser dine resultater sgu fornuftige ud Illusive. Jeg stoler i øvrigt pænt meget på dine matematik evner, så jeg sætter en deal op efter dem.

Tusind tak for hjælpen, også til alle andre der har kommenteret.

Bedste hilsner,

Mark P

Intuitivt synes jeg også tallene ser fornuftige ud. Forstår dog ikke hvorfor man vil have en sådan deal fra stakee's side. Er det fordi man ikke har rullen (burde vel kunne bankes op relativt hurtigt), eller er det pga manglende risikovillighed (hvilket givet Asgers eksempel på forrentningen heller ikke giver mening).

Hvis der følger coaching med som stakee virkelig føler giver added value, så giver det bedre mening, men ellers forstår jeg ikke at Sauce kan sælge det, da det nærmest ligner et rip off af stakee's.

@ Jensen

Altså en stake deal er jo som udgangspunkt næsten altid et spørgsmål om at hesten har skills men ikke rulle til at spille selv.

Hvis du mener setuppet er et rip off fra stakerens side så tror jeg måske ikke helt at du har forstået matematikken bag. Det vi sigter efter her er at staker og hest deler profitten 50/50 hvilket vel betegnes som helt standard og langt fra et rip off?

Grunden til at splitten i de enkelte intervaller bliver mere end 50% for stakeren er for at udjævne de gange hesten går stuck i et givet interval. Vi kunne også køre en normal deal med make up, men det går ikke i dette tilfælde da hesten har brug for jævnlige udbetalinger til udgifter.

Giver det mening?

@ Knish

Jeg er helt med på at det større split til fordel for staker, er det som skal kompensere for at dealen stadig giver ca 50/50 efter de gange hesten går stuck.

Min tanke er bare (og måske en arbejdsskade som økonom) at hvis det langsigtede afkast på en aktieinvestering i et bredt index er ca. 7% (her kan hesten også gå stuck i et givent interval, selvom det er knap så relevant her), så er Illusives 180% afkast jo sygt godt, og ligner overnormal profit, hvilket der ikke burde være i et efficient marked.

Det sagt, så har staker selvfølgelig en anstændigt risiko på at hesten ikke chipdumper eller laver andre narrestreger, men det kan den ærlige hest selvfølgelig ikke bruge til ret meget.

Så, overall er det nok mere de 50/50 der som markedsstandard er sat forkert imo. Man kan ihvertfald sige at det er meget pudsigt at den helt korrekte fordeling lige præcis er et pænt rundt 50/50, og ikke noget helt andet :-)

Een ting er selvfølgelig at markedet her ikke er efficient, men de 50/50 er nok ca lige så random, som at vi pokerspillere (som den gamle mand fra Skødstrup - U know who - plejer at sige) har været heldige med at raken blev sat til 5% med en cap på 3USD, da gamet nok aldrig var blevet til det som det endte med, såfremt den havde heddet 10% og 10USD.

Håber ovenstående giver mening :-)

Jeg ved egentlig ikke om det er et efficient marked eller ej. Men der er jo en temmeligt markant pointe i, at det er ret svært at opstøve en god pokerspiller, der ingen penge har. Det er selvsagt en gigant forretning, hvis der bare stod horder af skilled gutter klar, der bare kunne sidde at rense - men den slags hænger ligesom ikke bare på træerne. Heraf følger, at 50/50 longterm måske ikke er helt off.

Kunne den ikke vendes om?

Altså at der netop ikke står horder klar, fordi dealen ikke er god nok for hestene (uagtet at den primære grund vel er at vindende spillere sjældent har behovet for en staker)?

I bund og grund, så ændrer det vel heller ikke på dealen om der er 1000 vindende spillere der gerne vil have denne deal, eller om der kun er en enkelt. Payoff skal vel være den samme mellem hesten og stakeren ideelt set, og i et stramt udbud af heste, så skal det vel snarere være i hestens favør?

Generelt bryder jeg mig heller ikke om når noget utilsigtet bliver markedet, som de 50/50, da det nærmest umuligt kan være den rigtige fordeling, men blot en random pæn fordeling.

Anyway, det var ikke for at afspore tråden, eller andet, undrede mig blot over fordelingen, og det umiddelbart pænt store afkast til staker.

Tråden var jo done, så det er da et fint derail. Og tak for "det omvendte perspektiv". Det havde jeg ikke lige overvejet.