Hvordan finder man sidelængde + vinker

Hey Pn.

Hvordan finder man sidelængder og vinkler i en ligebenet trekant når arealet er 32000 m2?

På forhånd tak :)

Kan man ikke uden mere info.

Okay, det er for min mosters knægt, der går i 9 klasse. Hun siger, at der ikke er givet yderligere info...

Jeg må søge videre!

Problemet er vel at der kan være flere forskellige ligebenede trekanter med areal på 32000 m2.

Ligningen for arealet af en ligebenet trekant er jo h*g*0,5 , så vi mangler lige lidt mere info.

Du får opgaven her om to min.

... og lad ham tegne den i geogebra....

Niklasvs skrev:Hey Pn.

Hvordan finder man sidelængder og vinkler i en ligebenet trekant når arealet er 32000 m2?

På forhånd tak :)

Mon ikke, der menes ligesidet.

Nogle gange skal man ikke tænke over svaret men over spørgsmålet.

opg. 3.6 tænker jeg.

Lad ham tegne en ligebenet trekant, i geogebra, der har et areal på 32.000. Mål vinklerne. Vis det og smid det ind i din opgave....

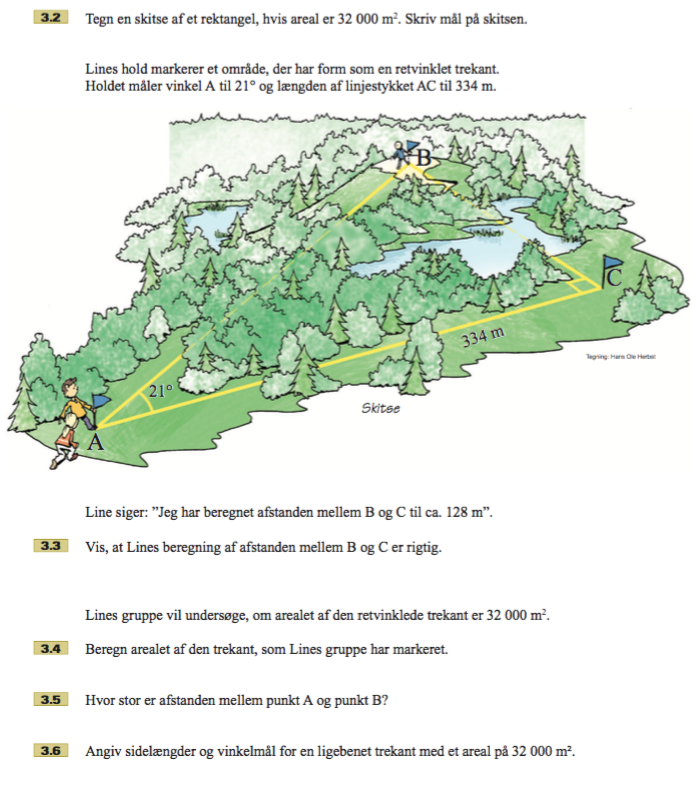
Ok, der spørges kun efter én løsning.
Retvinklet trekant, dvs vinkler 90,45,45.
Kateters længde a:
1/2 * a * a = 32000, dvs a = kvadratrod (64000)
Hypotenusens længde c: brug pythagoras.

Niklasvs skrev:Hey Pn.

Hvordan finder man sidelængder og vinkler i en ligebenet trekant når arealet er 32000 m2?

På forhånd tak :)

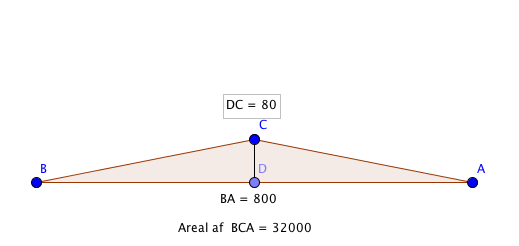
Overraskende simpelt måtte man lige tænker lidt over det. Du skal bare vælge en tilfældig trekant med det areal. Hvis du nu vælger en 80X800 rektangel lad os sig 80 i top og 800 i sider.

Så laver vi en ligeberettigelse trekant ud af den.

40 i top og stadig 800 lang. Så må det være rimeligt simpelt at finde siden c og vinklerne.

PN skuffer aldrig! Takker

@Nikas

Husk nu at en problemregning ikke går ud på at svare rigtigt. Det går ud på at vise at du svare rigtigt. Han får 0 point, hvis han smider Henrys eller Hermods løsninger ind.

hermod skrev:

Overraskende simpelt måtte man lige tænker lidt over det. Du skal bare vælge en tilfældig trekant med det areal. Hvis du nu vælger en 80X800 rektangel lad os sig 80 i top og 800 i sider.

Så laver vi en ligeberettigelse trekant ud af den.

40 i top og stadig 800 lang. Så må det være rimeligt simpelt at finde siden c og vinklerne.

Tænker at han mener.

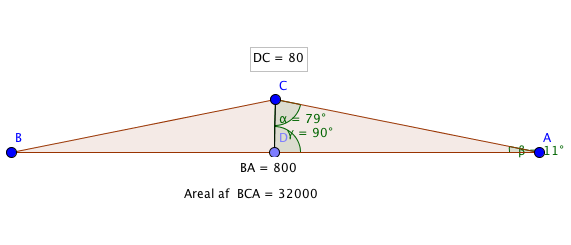
Du laver den 80*800

Så måler du/ regner vinklerne på den ene af de to retvinklede trekanter

Niklasvs skrev:Okay, det er for min mosters knægt, der går i 9 klasse. Hun siger, at der ikke er givet yderligere info...

Jeg må søge videre!

Nu er der allerede kommet fine løsningsforslag, og det er en af de svære opgaver. Et godt råd vil være, at de træner i at læse opgaveformuleringen, da der som i dette tilfælde oftest kan læses løsningsmuligheder ud fra den. I dette tilfælde at der findes (uendeligt) mange af de trekanter.

henry skrev:

Fatter intet.

Jamen jeg har da også fået en del rødvin :-)

Tankegangen man skulle følge døde også på et tidspunkt, da jeg var i tvivl om hvorvidt man kender til Sinus og cosinus-relationerne i 9. klasse.

*Man kender cos/sin/tan for retvinklede trekanter i 9. klasse... Eller burde!

hermod skrev:
Jamen jeg har da også fået en del rødvin :-)
Tankegangen man skulle følge døde også på et tidspunkt, da jeg var i tvivl om hvorvidt man kender til Sinus og cosinus-relationerne i 9. klasse.

Det gør man. Jeg kan godt følge dig, du laver rektangel med dobbelt areal, trekant i det, virker fint. Kan beregnes med trigonometri eller blot tegnes og måles som det tidligere er vist

Giver det point at tegne en trekant og måle vinklerne?

henry skrev:Giver det point at tegne en trekant og måle vinklerne?

Ja. En tegning i et it-program er lig med en udregning.

Problemregningen har ændret sig til at kunne løse opgaverne vha. it redskaber / hjælpemidler, frem for den mere teoretiske tilgang som tidligere.

Denne opgave var det første år hvor cos/sin/tan var en del af pensum i 9. klasse. Det er lidt presset at regne vinklerne i en retvinklet trekant, da men skal bruge den inverse værdi.. ( i forhold til den normale formelsamling). Derfor er det klart nemmest at tegne/ måle denne opgave i geogebra.

Perro skrev:

Denne opgave var det første år hvor cos/sin/tan var en del af pensum i 9. klasse. Det er lidt presset at regne vinklerne i en retvinklet trekant, da men skal bruge den inverse værdi.. ( i forhold til den normale formelsamling). Derfor er det klart nemmest at tegne/ måle denne opgave i geogebra.

Du har helt ret men, det er en smagssag, om du er mest tryg ved at anvende geogebra eller pythagoras. Din tankegang giver udtryk for en teoretisk forståelse og opgaven. Elever der er presset i denne opgave, har sjældent det overblik. Omvendt er det lige præcis meningen med opgaverne, at den kan løses via flere forskellige metoder.

Perro skrev:Du har helt ret men, det er en smagssag, om du er mest tryg ved at anvende geogebra eller pythagoras. Din tankegang giver udtryk for en teoretisk forståelse og opgaven. Elever der er presset i denne opgave, har sjældent det overblik. Omvendt er det lige præcis meningen med opgaverne, at den kan løses via flere forskellige metoder.

Uden yderligere argumentation er din tegning dog ikke til fuldt pointtal, da du ikke har angivet vinklernes størrelse og ikke har målt sidelængderne

EDIT: Henrys løsning må være den letteste og kan klares med en almindelig lommeregner vha kvadratroden og formelsamling.

Tegn et kvadrat. Kvadratets areal: 64.000. Hver side i kvadratet har derfor en længde på √(64000)=252.982212813

Slå en diagonal i kvadratet og vi får (2) ligebenede trekanter med areal på 32.000 hver.

Trekanten har en vinkel på 90 grader og de 2 andre vinkler er på 45 grader, da kvadratet har 4 hjørner med hver 90 grader.

Vha almindelig lommeregner kan sidelængderne beregnes. 2 sider kender vi allerede: 2 sider á √64000 = 252.982212813

Den sidste side er (hypontenusen = a^2 + b^2 = c^2) = (√64000)^2 + (√64000)^2 = 128000. C^2=128000, C= 357.7708764

Evt kontrol vha formel for areal af trekant: (0,5*højde*grundlinie) = 0,5*252.982212813*252.982212813 eller 0.5*√(64000)*√(64000)=32000

Alternativt med hypotenusen som grundlinie= 0,5*(357.7708764/2)*357.7708764 eller 0.5 × (√(128000)/2) × √(128000)

Edit: jeg ved godt at det ikke er løsningen men løsningsforslag der diskuteres i tråden.