Hvordan reducere man den her? (matematik)

Er ved at finde skæringspunktet mellem to andensgradspolynomiumer, og kan simpelthen ikke finde ud af at reducere følgende:

-x^2+2x+6-2x^2+4x+2

-3x^2 +6x + 8

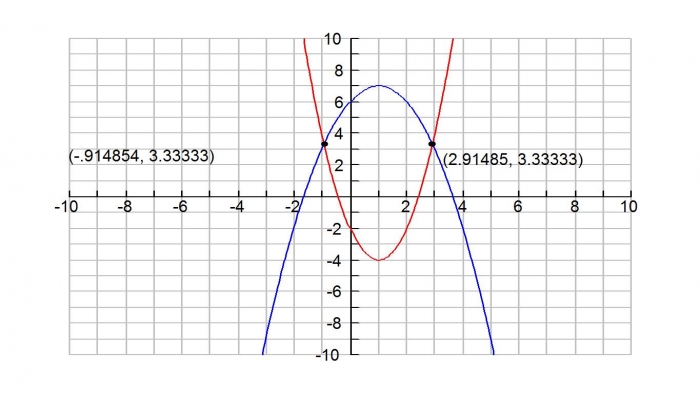
Ok, det fucker helt op!

her er min udregning

g(x) = f(x)
-x^2+2x+6= 2x^2-4x-2
-x^2+2x+6-(2x^2-4x-2)= 0
-x^2+2x+6-2x^2+4x+2= 0
-3x^2+6x+8= 0

Diskriminanten:
D= 6^2-(4*-3*8)
D = 132



Nulpunkterne:
x1 = (-6+ √132)/36 = 2,91

x2 = (-6- √132)/36 = -0,91

Skæringspunktet må derfor være: (HER DET FUCKER OP)

-x^2+2x+6

(0,91^2)+(2*-0,91)+6 = 5,0081

5,0081 passer med ingenting :(

(-(.914854)^(2) + 2*-.914854 + 6) er lig 3.3333 og ikke 5.0081

Y-koordinaten er ikke engang 3,3333 (ikke der de skærer).. wtf!!

Når du skal finde x1 og x2 dividerer du med 36 det er forkert - du skal dividere med 2a som er lig -6.

Jo for f(x)=-x^2+2x+6 og g(x)=2x^2-4x-2