Løsning til mindre matopgave?

Nogle der lige kan hjælpe med den her?

Opg:

Find højden i en ligesidet trekant med sidelængden 2a

Pythagoras

Jep self Pythagoras opgaven er fra et sæt udelukkende forkuserende på Pyt. Men hvordan skal den forstås? Vi ved jo at alle sider er lige lange og vinklerne lige store i en ligesidet trækant. Skal den bare beregnes a^2 + b^2 = 2c^2 kun skrevet a^2 da vi jo halverer grundlinjen for at danne en trekant ind i trekanten, så vi kan finde højden.

edit: manglede lige et par hatte

yderligere edit: jeg er helt gal på den, sidder sgu lige med for meget andet, mens jeg spiller klog!

hypotenusen er 2a, dens kvadrat er 4a^2.

h^2= 4a^2-a^2 = 3a^2

h= kvrod(3a^2). kvadratrodsregel: produktet af de enkelte kvadratrødder. h=kvrod(3a^2)= kvrod(3)*kvrod(a^2)= kvrod(3)*a

Manner, er jeg helt gal på den??? Næh, ikke nu ser jeg i næste post.

Pythagoras er kun til retvinklede trekanter, no?

En ligesidet trekanter har jo samme sidelængder.

Wiki skriver at højden burde være sidelængde gange kvrod(3)/2.
Så får vi a*kvrod(3), hvis jeg husker mine regneregler rigtigt.

I har self ret. Vi deler bare den ene side op i to og får to kateter a og b og en hypotenuse c. Hypotenusen ved vi er 2a, og den ene katete er a.
Derfor må højden være: 2a^2-a^2 = b^2
Altså 4 = b^2
Og b = 2.

Franneren skrev:I har self ret. Vi deler bare den ene side op i to og får to kateter a og b og en hypotenuse c. Hypotenusen ved vi er 2a, og den ene katete er a.
Derfor må højden være: 2a^2-a^2 = b^2
Altså 4 = b^2
Og b = 2.

nej, for (2a)^2= 4a^2

a^2+h^2=2a^2
h=1.73a

e: typo da jeg tastede ind på lommeregneren.

adswx skrev:a^2+h^2=2a^2
h=1.41a

du mangler paranteser om din 2a

moktar skrev:

nej, for (2a)^2= 4a^2

Hmm jeg får at den giver: b^2 = kvrod(2a^2 - a^2) = b = kvrod(2^2 - 1^2) = 1,73 ??? Taster på min lommeregner kvrod(2^2-1^2) er dette forkert? det giver 1,73a

Resultatet skal jo ligge mellem 1a og 2a da hypotenusen her er 2a, som jo altid er den længste i en retvinklet trekant.

Kommer lige i tvivl. Havde for ikke så længe siden nogle elever der døjede med samme opgave. Jeg kigger lige på det senere :)

Der bliver rodet godt og grundigt rundt i regneregler ovenfor :) ♥

(a)^2 + (h)^2 = (2a)^2 <=>

h^2 = 4*a^2 - a^2 <=>

h^2 = 3*a^2 <=>

h = sqr(3a^2) = sqr(3)*a = 1,73a

Gramm0 er spot on. Det der voldte problemer for eleverne (og åbenbart overtegnede :)) var, at kende forskel på 2(a^2) og (2a)^2, samt kvadratrod(3a) og kvadratrod 3*(a).

Nogle endte med at køre nogle tests i excel, og ville teste følgende efter deres lille fehler: '1'. 'Større end 1'. 'Mindre end 1'. Samt 'Skæve/komma-tal'. Det så nogenlunde sådan ud:

Takker alle der deltog i debatten og hjalp med svaret.

@Dieb i må gerne slette tråden nu hvis det er.

Brozze skrev:

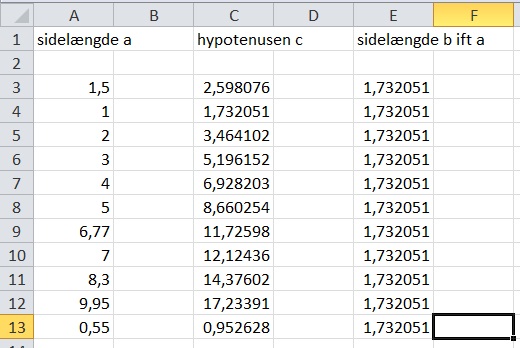
Takker alle der deltog i debatten og hjalp med svaret.

@Dieb i må gerne slette tråden nu hvis det er.