Mikroøkonomi/VØ opgave

Har fået dette spørgsmål og jeg ved at svaret skal være L=6. Men når jeg selv prøver at løse den, så kommer jeg frem til L=12. Nogen som har et forslag til en fremgangsmåde, hvor man får L=6?

2*1²*16= 32

20 - ½ * 32 = 20 - 16 = 4... sikker på den ikk skal give 4??

regner med du har sagt Q = 2*1 derefter ² og så ganget med 16, så får du 64
20-½*64 = 20-32 = -12... så du har vel ikke fået +12 ?

Nej, jeg får det til 12.

Det du finder er jo P?

Vores underviser har lagt svarene fra sommereksamen 2013 ud og der skriver han som svar på spørgsmålet:

MRPL=W => L=6

Nu er det jo ikke oplyst, men P=Pris på produktet (til kunderne), og Q=mængde. Og så skal man finde det optimale pris/omkostningsniveau, når timelønnen er 16.

Jeg får det også umiddelbart til 6. idet der kan produceres 2 i timen (L=Q/2), og oms-omk er 72 ved L=6 (Q=12)

Omsætning er Q*P

DB er Oms-w

Jeg kan ikke huske formlen for at finde max DB (jeg mener du bruger 2 ligninger med 2 ubekendte, men jeg kan ikke huske hvilke 2 ligninger), men jeg lavede nedenstående tabel i Excel, hvor man kan se, at max DB fås ved L=6, Q=12, hvor DB bliver 72:

Q P oms w DB L
0 20 0 0 0 0
1 19,5 19,5 8 11,5 0,5
2 19 38 16 22 1
3 18,5 55,5 24 31,5 1,5
4 18 72 32 40 2
5 17,5 87,5 40 47,5 2,5
6 17 102 48 54 3
7 16,5 115,5 56 59,5 3,5
8 16 128 64 64 4
9 15,5 139,5 72 67,5 4,5
10 15 150 80 70 5
11 14,5 159,5 88 71,5 5,5
12 14 168 96 72 6
13 13,5 175,5 104 71,5 6,5
14 13 182 112 70 7
15 12,5 187,5 120 67,5 7,5
16 12 192 128 64 8
17 11,5 195,5 136 59,5 8,5
18 11 198 144 54 9
19 10,5 199,5 152 47,5 9,5
20 10 200 160 40 10
21 9,5 199,5 168 31,5 10,5
22 9 198 176 22 11
23 8,5 195,5 184 11,5 11,5
24 8 192 192 0 12


Hmmm, jeg kan så se, at det ikke ser helt godt ud på skærmen. Jeg har et excel ark du kan få, hvis det har interesse.

Har lavet et billede i stedet: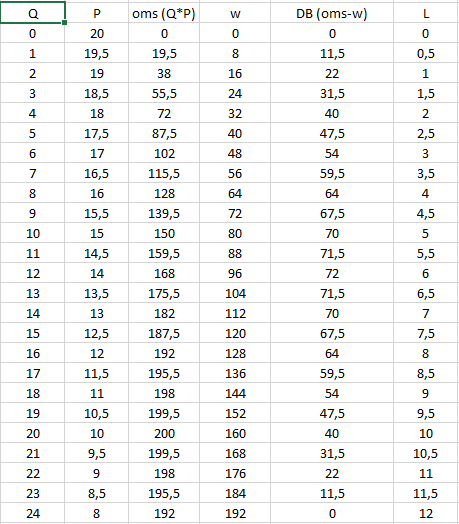

Fandt lige nogle formler i en gammel opgave:

Det første man gør er at finde hældningsgraden(a) ved formlen a=P1-P2/Q1-Q2 ud fra formlen P(pris)=a*Q(mængde)+b, hvor henholdsvis (P1,Q1) og (P2,Q2) er givne punkter. Derefter finder man skæringen på y-aksen(b) ved formlen b=P-a*Q.

Det giver:
a=-0,5
b=20
(disse er faktisk givne ved formlen for P i opgaven, så vi behøver ikke bruge delta)

For så at finde den mest rentable afsætning skal man finde Marginal indkomsten (MR) og Marginal omkostningerne (MC). MR er nemt fundet idet MR=P med den dobbelte hældning:
MR=2*a*Q+b
MC findes ved formlen:
MC=(delta)TVC (Totale variable omkostninger)/(delta)Q
Da L=Q/2 vil L ændre sig 0,5 hver gang Q ændrer sig 1. Og da 1*L koster 16 er (delta)L = 8 for (delta) Q = 1, og derved bliver MC=8.


Så nu ved vi, at vi skal finde Q for MR=8, for at finde ligevægtsintægten (MR=MC).
Derved fås:
8=2*-0,5*Q+20 => -Q+20=8 => Q=12

Da L=Q/2 vil det optimale scenarie være L=12/2=6

Torstens rammer den :)

Wow hold da op, det var noget af en forklaring!
Virkelig god stil at du gider bruge tid på det :)

Er det muligt at at forklar denne som lidt mere detaljeret(hvis det er muligt)?

MC=(delta)TVC (Totale variable omkostninger)/(delta)Q
Da L=Q/2 vil L ændre sig 0,5 hver gang Q ændrer sig 1. Og da 1*L koster 16 er (delta)L = 8 for (delta) Q = 1, og derved bliver MC=8.

@Ace
Alt du skal huske er den dobbelte hældningskoefficient. Så får man næsten det samme som Noctra først påpegede bortset fra, at ligningen kommer til at hedde: (20-1Q)*(2K^2)=16 => 24=4L => L=6.
Du må obv ikke hænge mig op på det, men er næsten sikker på det er sådan de forventer opgaven løst.

Sådan, nu er jeg helt med :) Var som I sagde, den dobbelte hældningskoefficient jeg havde glemt at tænke på.

Tak for hjælpen Noctra og FlaskeW :)

AceKiller88 skrev:

Er det muligt at at forklar denne som lidt mere detaljeret(hvis det er muligt)?

MC=(delta)TVC (Totale variable omkostninger)/(delta)Q
Da L=Q/2 vil L ændre sig 0,5 hver gang Q ændrer sig 1. Og da 1*L koster 16 er (delta)L = 8 for (delta) Q = 1, og derved bliver MC=8.

Tak, man kan altid bruge en ekstra forklaring, når man ik ligefrem er en haj til mikro :-)

Nu hvor vi er i gang, så har jeg et til spørgsmål.

Når man skal ind og regne i excel, så har jeg svært ved at se om jeg skal bruge nettonutidsværdi eller Nutidværdi. Nogen som kan forklar det simpelt?

Altså hvordan man på en opgave kan se om man skal bruge Netto.nutidsværdi eller Nutidsværdi?

F. eks som her:



Her skal man bruge nettonutidsværdi, men hvorfor kan man ikke bruge nutidsværdi?

Nettonutidsværdi forstås, så vidt jeg husker, bare som inflow minus outflow. Dvs. 30000*1.02^-1 + 30000*1.02^-2 + 30000*1.02^-3 - 60000

Hva med nutidsværdi, den tager ikke højde for outflow eller?

Er gået op for mig at du snakker om excel kommandoer, kender ikke den præcise forskel på de to. Jeg ville taste formlerne ind manuelt så jeg ved excel ikke screwer mig :)

Det er jeg aaaalt for doven til ;)

AceKiller88 skrev:
Nu hvor vi er i gang, så har jeg et til spørgsmål.

Når man skal ind og regne i excel, så har jeg svært ved at se om jeg skal bruge nettonutidsværdi eller Nutidværdi. Nogen som kan forklar det simpelt?

Altså hvordan man på en opgave kan se om man skal bruge Netto.nutidsværdi eller Nutidsværdi?

F. eks som her:



Her skal man bruge nettonutidsværdi, men hvorfor kan man ikke bruge nutidsværdi?

Forstår ikke helt hvorfor du skal gøre det så indviklet Torstens?

Optimale brug af arbejdskraft = MRPL = W
MR = 20 - Q
MPL = 2*1^2L differentierer og sæt lig 0.
MPL = 2
MRPL = =(20-Q)*2 =>
(20-(2*1^2L))*2 = -4*(L-10)

MRPL = W

-4*(L-10) = 16

L = 6