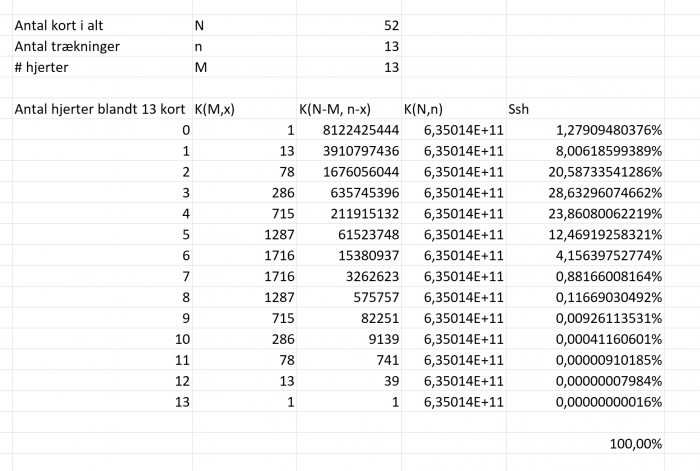
Med udgangspunkt i Heads up Omaha, hvad er de matematiske formler for, at kunne udregne flg.:
Spiller 1: xxxx
Spiller 2: xxxx
Board: xxxxx
Sandsynligheden for, at der imellem spillere og board er præcis 0-13 kort I samme kulør.
Skal bruge resultat for alle.
Nogen der kan hjælpe?
/Kasper
Regner det ikke yd ud men formoder at metoden er således:¨
Spiller 1: (13/52x11/50x(9/48x7/46
Spiller 2: 12/51x10/49x8/47x6/45
Board 3: 5/44x4/43x3/42x2/41x1/40
jeg er ikke nogen ørn til matematik længere så kan være off..
Edit:
Tror jeg er off - prøvede lige at regne på det og vi er nærmest ikke engang ude i promiller så nok ikke den metode.
Hej Kasper
Jeg skal nok lige sende svarene i aften eller i morgen tidlig afhængigt af, hvornår jeg får tid til at regne dem :-)
52/52 * 12/51 * 11/50 * 10/49 * 9/48 * 8/47 * 7/46 * 6/45 * 5/44 * 4/43 * 3/42 * 2/41 1/40 = Svar
GuldsmedeN skrev:52/52 * 12/51 * 11/50 * 10/49 * 9/48 * 8/47 * 7/46 * 6/45 * 5/44 * 4/43 * 3/42 * 2/41 1/40 = Svar
Spiller 1: 52/52 x 11/50 x 9/48 x 7/46=x
@Prangstar
Ja, så vidt jeg lige kan se, har vi lavet det samme regnstykke.
@OP
Du kan anse det som sandsynligheden for at trække 13 kort, hvor alle disse kort skal være af én kulør. Det første kort du trækker kan være et hvilket som helst, altså 52/52. Derefter skal du trække et af de resterende 12 kort fra den samme kulør ud af de resterende 51 kort, and so on. Det giver et grotesk lille tal, og selvfølgelig er sandsynligheden for det sker også uendeligt lille. Det svarer til at trække en überstraightflush :D
@guldsmeden @prangstar
Tak for input :-)
Hvad hvis det SKULLE være hjerter?
/kasper
Sandsynligheden for kun spar/hjerter/ruder/klør er symmetrisk, så du kan bare dividere den samlede udregnede sandsynlighed med 4, så får du sandsynligheden for en enkelt kulør.
Alternativt skal du rette første faktor i udregningen, så du ikke starter med 52/52 (altså første kort er ligegyldigt) til 13/52 svarende til du er ude efter en bestemt kulør.
Resultatet bliver det samme.
Forhåbentlig i tid til DSMPT´en.
Har arbejdet på det i over 2 år og har endelig fået det godkendt, så mangler bare de sidste finpudsninger og udregninger.
Men alt ser ud til, at være i orden; så I kan godt forvente lir ud over alle grænser!! :-)
/Kasper
@OP
Kan du præcisere dit spørgsmål lidt?
Har fordelingen mellem spillere og board nogen betydning? Eller er det grundlæggende bare "ud af 13 kort".
1. Spørger du efter den præcise sandsynlighed for en tilfældig kulør (minimum 1). F.eks en manglende kulør ud af 13 kort. dvs 0 ud af 13 (og videre for alle tal fra 0-13). Her vil den samlede sandsynlighed addere til mere en 100%, da der jo er 4 kulører, men antallet af 2 eller 3 kulører kan være ens. Der er således ikke generel symmetri i svarende mellem minimum 1 kulør og kulørerne hver for sig. Dette er kun tilfældet for tallene 7-13. Da der godt kan være 2 kulører med 6 kort.
2. Spørger du efter den præcise sandsynlighed for der er feks 8 af den mest hyppige kulør ud af 13 kort (og således fra 4-13). Dette har nok større relevans for poker, da man sjældent bekymrer sig om den kulør der er færrest af.
Denne sandsynlighed vil addere til 100%.
Bemærk at du indtil videre kun har fået svaret for tilfældet 13 ud af 13 kort.
For at finde sandsynligheden for at trække præcis x hjerter blandt 13 kort bruger vi den hypergeometriske fordeling med:
N = # kort i alt = 52
n = # trækninger = 13
M = # "rigtige kort" = # hjerter = 13
Lad X betegne antallet af trukne hjerter. Der gælder at:
P(X=x) = K(M,x) * K(N-M,n-x) / K(N,n)
Hvor: K(n,r) = n! / (r! * (n-r)!)
Så er det bare at regne løs, vi kan trække mellem 0 og 13 hjerter:
@rickrick
Takker for inputtet, jeg har netop haft en Excel-ekspert til, at vise mig hvordan det kan beregnes og jeg er kommet frem til det samme.
Det er for i øvrigt til et Omaha side bet....
/Kasper
kkdk skrev:@rickrick
Takker for inputtet, jeg har netop haft en Excel-ekspert til, at vise mig hvordan det kan beregnes og jeg er kommet frem til det samme.
Det er for i øvrigt til et Omaha side bet....
/Kasper
Så lidt, ellers siger du bare til, så sender jeg arket til dig :-)
