PNVA: Formel på antal kampe

Kære Matematiske Genier!

Nogen der kender en formel eller lign, som kan udregne kampe iht. nedenstående..

Fodbold 2 mod 2.
Alle skal møde hinanden, hvor alle når at være sammen med alle.
4 spillere = 3 kampe
5 spillere = 15 kampe
6 spillere = ???
7 spillere = ???
Netop dette jeg mangler formel til :-)

Håber nogen kan hjælpe.

PFT
Cinco

4 spillere = 1+2+3 = 6
5 spillere = 1+2+3+4 = 10
6 spillere = 1+2+3+4+5 = 15
7 spillere = 1+2+3+4+5+6 = 21

Hvis det er 2 mod 2 er der kun en kamp ved 4 spillere. Eller hst du skrevet forkert?

Argyle_DK skrev:
Hvis det er 2 mod 2 er der kun en kamp ved 4 spillere. Eller hst du skrevet forkert?

Argyle_DK skrev:
Hvis det er 2 mod 2 er der kun en kamp ved 4 spillere. Eller hst du skrevet forkert?

Edit: Misforstod spørgsmålet! Jeg kan dog informere om, at 6 deltagere giver 105 kampe og 7 deltagere 210 kampe :)

Har lavet formlen i Excel, men fatter ikke at udtrykke den i X og Y, da den er eksponentiel.. :)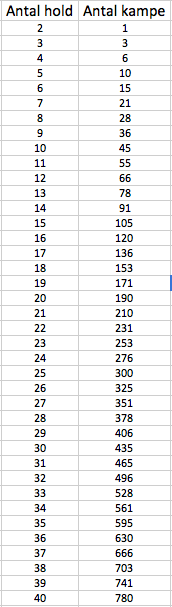



Let me know, hvis du mangler udregninger for mere end 40 hold.. :)

@ tightgirl-
tror du har glemt at tage højde for at alle skal være sammen med alle. det scenarie du har er med faste hold hvor der ikke skiftes medspiller

ved 2 hold giver det følgende:

1+2 vs 3+4
1+3 vs 2+4
1+4 vs 2+3

altså 3 kampe ved 4 spiller som OP også skriver.

4 spillere: 3*1 = 3
5 spillere: 4*3+3*1 = 15
6 spillere: 5*6+4*3+3*1 = 45 kombinationer

Manglede lige for 7: 6*10+5*6+4*3+3*1 = 105

Ved 5 spillere kan der laves 4+3+2+1 = 10 forskellige holdkombinationer

Kan skrives som ((5 - 1) * 5) / 2 = 10

Hvert hold kan mødes mod antal af kombinationer af de sidste 3 spillere (3+2+1)/2 = 3 hold.

Kan skrives som (((5 - 3) * (5 - 2)) / 2) = 3

Ganges sammen og deles med to

(10 * 3) / 2 = 15 kombinationer

Formel-ish:
((((Antal hold - 1) * Antal hold) / 2) * (Antal hold - 3) * (Antal hold - 2) / 2))) / 2

kan sikkert gøres nemmere nu jeg tænker over det, men jeg får i hvert fald samme resultater som bechorff

Harry Butt skrev:
Ved 5 spillere kan der laves 4+3+2+1 = 10 forskellige holdkombinationer

Kan skrives som ((5 - 1) * 5) / 2 = 10

Hvert hold kan mødes mod antal af kombinationer af de sidste 3 spillere (3+2+1)/2 = 3 hold.

Kan skrives som (((5 - 3) * (5 - 2)) / 2) = 3

Ganges sammen og deles med to

(10 * 3) / 2 = 15 kombinationer

Formel-ish:
((((Antal hold - 1) * Antal hold) / 2) * (Antal hold - 3) * (Antal hold - 2) / 2))) / 2

kan sikkert gøres nemmere nu jeg tænker over det, men jeg får i hvert fald samme resultater som bechorff

Jeg takker mange gange for hjælpen..
Det er nemlig lidt tricky, når alle skal være sammen med alle - Mod alle.

Jeg må igang med et skema :-)

Harry Butt det er forkert.
I tager udgangs punkt i 2/4 2/5 osv. Som man kender det fra fodboldkampe på oddset.
Men her er det matchups hvor alle skal spille mod alle af hold med 2, som ikke er faste hold.

Sjovt spørgsmål, hvor svaret er langt fra oplagt synes jeg. Jeg er enig med Harry Butt og underk.

Det bliver intuitivt klart, hvis man går igang med at opstille kombinationer, hvor de to første tal angiver hold 1 og de to næste tal angiver hold 2. Lad N angive antallet af spillere.

N=4: Her er der 4 spillere og de mulige kombinationer er:

3456

3546

3645

Altså 3*1 = 3 kampe.


N=5: Nu er der 5 spillere og kombinerer vi spiller 2 (den nye spiller) med alle spillere og alle kombinationer af modstandere får vi:

2345
2346
2356

2435
2436
2456

2534
2536
2546

2634
2635
2645

Da spiller 2 pr. definition har spillet med alle kombinationer af spillere mod alle kombinationer af spillere har vi dækket alle muligheder minus dem, hvor spiller 2 ikke er med, men de er præcis dækket for N=4, dvs 12 + 3 = 15 kampe.


N=6: Nu er der 6 spillere og kombinerer vi spiller 1 (den nye spiller) med alle spillere og alle kombinationer af modstandere får vi:

1234
1235
1236
1245
1246
1256

1324
1325
1326
1345
1346
1356

1423
1425
1426
1435
1436
1456

1523
1524
1526
1534
1536
1546

1623
1624
1625
1634
1635
1645

Da spiller 1 pr. definition har spillet med alle kombinationer af spillere mod alle kombinationer af spillere har vi dækket alle muligheder minus dem, hvor spiller 1 ikke er med, men de er præcis dækket af N=4 plus N=5 dvs 30 + 12 + 3 = 45 kampe


For hvert N er der (N-1) blokke og mulighederne i hver blok (de sidste 2 tal) er kombinationer af par ud af (N-2) tal, dvs.:

Antal kampe = Sum_{i=4}^{N} (i-1)*Komb(i-2,2)

rickrick nailed it, have fun :)

MoPe skrev:
rickrick nailed it, have fun :)