Sandsynligheds regning/ blak jack

Hvordan regner man sandsynligheden ud for at tabe 8 gange i træk i bj.
Og nej har ikke lige tabt 8 gange i træk :)

Kommer vel an på hvor godt du spiller black jack?

SpartacusDK skrev:
Kommer vel an på hvor godt du spiller black jack?

Hvis man spiller optimalt, og vi snakker euro bj

Hvorfor vil du vide det?

Et præcist tal kan du sikkert ikke få...

Men en hurtig tanke er, at TBP er lige under 100% (taget ud fra, at det er muligt at få TBP lige over 100% ved at tælle kort). Dvs I er meget tæt på at være even i chancer... Lad os give dig 49.5% chance on average så... Det er sikkert ikke helt skævt...

Så er chancen for at tabe de NÆSTE 8 i træk: 0.495^8 = 0.36% eller ca 1 af 278 gange.

Chancen for at tabe 8 i træk er 0.495^7 = 0.73% eller ca 1 ud af 137 gange.

Så noget i det leje... Hvis du kan bruge det til noget :)

Da de fleste spiller noget dårligere, så er tallet nok en smule lavere :)

Zorro@
Det var lige nøjagtigt underdog med 49.5 jeg mente.
Kunne bare ikke regne måden
Tak for hjælpen

Er det så samme chance for gevinst? ;-)

Martingale projekt roedroed?!

Granaten11 skrev:
Martingale projekt roedroed?!

Skal jo have reddet min 2 mil i tab i bj ind igen :)

Zorro har ret, bortset fra at han har regnet chancen ud for at vinde 8 i træk. Du skal i stedet udregne (1-0.495)^7 og ^8. Tallene er dog nok meget ens alligevel :-)

@Razga

Korrekt... Klokken er over midnat, og jeg har været i skole fra kl lort i morges :)

0.505^8 = 0,42% eller 1 ud af 236.
0.505^7 = 0,84% eller 1 ud af 119.

Igen så træk lidt fra, fordi folk så godt som aldrig spiller optimalt...

Tak til Razga for at holde mig i ørerne :P

Jeg har en plan, en Black Jack plan... :)

roedroed skrev:
Jeg har en plan, en Black Jack plan... :)

En plan der der efterlader dig med 0 kr efter i snit 236 forsøg.

^^^^ this! ;-)

DarkXoiX skrev:

roedroed skrev:
Jeg har en plan, en Black Jack plan... :)

En plan der der efterlader dig med 0 kr efter i snit 236 forsøg.

Alle der har succes har taget chancer :) :) :)

zorro razga.
Som jeg forstå regnstykket, så er chancen for at huset vinder 8 i træk, 1 ud af 137.
Chancen for at jeg taber 8 i træk er, 1 ud af 119. differencen er split??

Regnestykket er nok lidt mere kompliceret. Gætter på man i de fleste spil er dårligere end 49,5% da man i enkelte spil fx 11 mod 5 kan doble og har super odds

Lige 2 spørgsmål mere.
Er de 1 ud af 119, nå man rammer 119 eller fra 119. Altså taber man 8 gange i træk fra 111 eller starter tabs runden på 119.
Hvordan regner man sandsynligheden ud for at tabe 8 gange i træk ud af maks 15 træk.
Vi snakker stadig 49.5 underdog

Lakini9 skrev:
Regnestykket er nok lidt mere kompliceret. Gætter på man i de fleste spil er dårligere end 49,5% da man i enkelte spil fx 11 mod 5 kan doble og har super odds

Udregningen med de første 49,5% er det inkluderet man kan splitte/doble, tro mig, hvor godt du end spiller - vil casinoet altid være i favør.

Det jeg med på. Tror bare ikke man kan regne det på samme måde som fx at spille rød/sort på rouletten.

Min tese er at det er nemmere at tabe 8 spil i streg på Bj end på roulette. Tilgengæld vil der også være perioder hvor man vinder mere, pga doble-split-Black Jacks

Lakini9 skrev:
Min tese er at det er nemmere at tabe 8 spil i streg på Bj end på roulette. Tilgengæld vil der også være perioder hvor man vinder mere, pga doble-split-Black Jacks

Hvilket obv. er korrekt.

For at have 49% (eller hvad man ender på med perfekt blackjack) kræver det man splitter/dobler på de korrekte tidspunkter.

Derfor vil din chance for at vinde hånden før kortene deles nok nærmere være 40-45%, hvilket gør det væsentligt lettere at tabe 8 i træk.

DarkXoiX skrev:

Lakini9 skrev:
Min tese er at det er nemmere at tabe 8 spil i streg på Bj end på roulette. Tilgengæld vil der også være perioder hvor man vinder mere, pga doble-split-Black Jacks

Hvilket obv. er korrekt.

For at have 49% (eller hvad man ender på med perfekt blackjack) kræver det man splitter/dobler på de korrekte tidspunkter.

Derfor vil din chance for at vinde hånden før kortene deles nok nærmere være 40-45%, hvilket gør det væsentligt lettere at tabe 8 i træk.

slap nu lidt af med de postulater, man skal sagt suseme være elendig til bj for kun at have 40% vinder chance. Nu er der selvfølgelig en hel del forskellige bj regler. Men hvis man spiller optimalt så hedder den ca 49.5% mod husets 50,5%. Realistisk er det nok nærmere 49.3% mod 50.7%.
roulette og bj har tæt på samme odds, men det er selvfølgelig pænt svært at ændre sine odds i roulette.

Lakini9 skrev:
Min tese er at det er nemmere at tabe 8 spil i streg på Bj end på roulette. Tilgengæld vil der også være perioder hvor man vinder mere, pga doble-split-Black Jacks

Den har jeg sku svært ved at se odds er vel odds.
Men okay lidt ret har du, da roulette har minimal bedre odds :)

roedroed skrev:

DarkXoiX skrev:

Lakini9 skrev:
Min tese er at det er nemmere at tabe 8 spil i streg på Bj end på roulette. Tilgengæld vil der også være perioder hvor man vinder mere, pga doble-split-Black Jacks

Hvilket obv. er korrekt.

For at have 49% (eller hvad man ender på med perfekt blackjack) kræver det man splitter/dobler på de korrekte tidspunkter.

Derfor vil din chance for at vinde hånden før kortene deles nok nærmere være 40-45%, hvilket gør det væsentligt lettere at tabe 8 i træk.

slap nu lidt af med de postulater, man skal sagt suseme være elendig til bj for kun at have 40% vinder chance. Nu er der selvfølgelig en hel del forskellige bj regler. Men hvis man spiller optimalt så hedder den ca 49.5% mod husets 50,5%. Realistisk er det nok nærmere 49.3% mod 50.7%.
roulette og bj har tæt på samme odds, men det er selvfølgelig pænt svært at ændre sine odds i roulette.

Jeg snakker om at vinde eller tabe hånden, snakker ikke om udbetalingsprocent. En stor del af din "juice" kommer fra doblinger og splits.

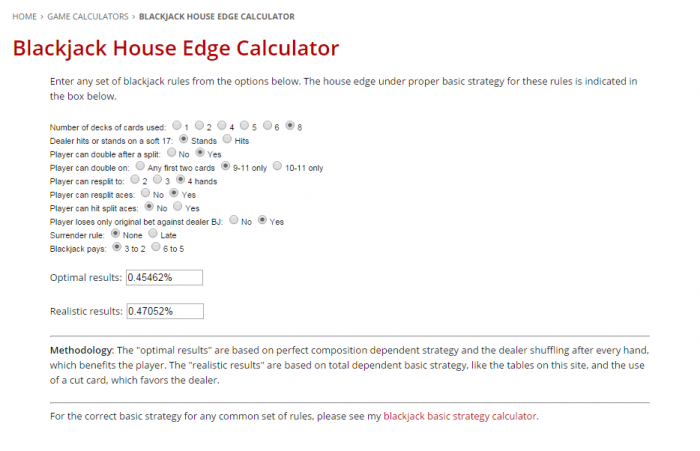
forstå godt hvad du mener med at vinde hånden kontra udbetaling.
Men der er meget lagt ned til 40% du kommer ikke under 47%, men der er selvfølgelig langt fra 49.5% og til 47%

Men havde ikke lige tænkt over det med at vinder chancen bliver forringet af at man ikke dobler

Roedroed - kan du ikke se forskellen på vundne hænder, og den egentlige house-edge?

Du vil vinde færre hænder end din edge, hvilket er negativt for et evt. Martingale-system.

Det er muligt du har 47% udbetaling, men du vil stadig ikke vinde 47% af hænderne.

roedroed skrev:
zorro razga.
Som jeg forstå regnstykket, så er chancen for at huset vinder 8 i træk, 1 ud af 137.
Chancen for at jeg taber 8 i træk er, 1 ud af 119. differencen er split??

Glem den første udregning med 1 ud af 137... Jeg kom der til at lave udregningen for, at du VINDER 8 i træk :)

Det er nr 2 udregning med 1 ud af 119, der er chancen/risikoen for, at du TABER 8 i træk :)

roedroed skrev:
Lige 2 spørgsmål mere.
Er de 1 ud af 119, nå man rammer 119 eller fra 119. Altså taber man 8 gange i træk fra 111 eller starter tabs runden på 119.
Hvordan regner man sandsynligheden ud for at tabe 8 gange i træk ud af maks 15 træk.
Vi snakker stadig 49.5 underdog

Det vil gennemsnitligt ske 1 ud af 119 gange... Hvad du har gjort i fortiden er irrelevant, så den sats er konstant, uanset hvor mange gange du har spillet. Det betyder ikke, at din risiko bliver større, fordi du har undgået det 1, 15 eller 111 gange først.

På samme måde kan du heller ikke føle dig sikker, bare fordi du måske taber de allerførste 8 hænder. Det kan sagtens ske igen lige bagefter. Chancen for at undgå det bliver ikke større af den grund.

Så det hele er gennemsnitligt. De der "runder", du snakker om, eksisterer ikke...

roedroed skrev:
Lige 2 spørgsmål mere.
Er de 1 ud af 119, nå man rammer 119 eller fra 119. Altså taber man 8 gange i træk fra 111 eller starter tabs runden på 119.
Hvordan regner man sandsynligheden ud for at tabe 8 gange i træk ud af maks 15 træk.
Vi snakker stadig 49.5 underdog

Nu bliver du lidt mere kompliceret :)

Sandsynligheden for at tabe 8 gange i træk ud af 15 forsøg er lig med 1 minus sandsynligheden for, at det ikke sker (Vi forudsætter her, at du STOPPER efter 15 spil, unaset om du har tabt eller vundet det sidste. Dvs du i princippet kan have tabt 7 i træk på det tidspunkt, og så betragter vi det stadig som om, at du undgik at tabe 8 i træk, og det dermed er en succes. Det vil du nok næppe i praksis betragte det som værende, da dit underskud i så fald stadig er kæmpestort ;) ) :

Sandsynligheden for at undgå at tabe de næste 8 i træk: 1-0.42% = 99.58%

For, at du kan "nå" at tabe 8 i træk inden 15 spil er afviklet, så skal din uheldige streak starte senest med det 8.spil.

Så ligningen må være noget i retning af: 1-(0.9958^8) = 3.31%

Så din risiko for at tabe 8 i træk, hvis du spiller præcis 15 spil (og stopper uanset om du er på en losing streak, dvs du kan sagtens være i minus efter de 15 spil, selvom du har undgået at tabe 8 i træk), er 3.31% eller 1 ud af 30 gange.

----

EDIT: Og ud af de 30 gange er det kun 50/50, om du har vundet det sidste spil. Du stopper jo efter 15 spil, uanset hvordan det er gået. Dermed er sandsynligheden for, at du er i minus langt større end de 3.31%. Det er ret vigtigt, så det håber jeg, at du er med på :)

Zorro.
Nu er det lidt af et martin gale projekt.
Det jeg mener med maks 15 spil er. Jeg skal vinder den 8 hånd. Det vil sige at hvis jeg vinder de første 7 hænder og taber den 8 hånd, så stopper projektet på hånd nummer maks 15. Hvis jeg vinder inden den 15 hånd så stopper det der.
Altså maks 15 hænder med en vinder hånd som den sidste, og mindst 8 hænder med en vinder hånd som den sidste

darkxoix@
du misforstår vist skemaet jeg satte ind.
Der er ingen tvivl om at der er stor forskel på om du doubler eller ej. Men man kommer aldrig derned hvor du snakker om. Med mindre man er sygelig fuld.
men nu doubler man også i mit projekt

Jeg er stadig ikke 100% med, for kan stadig læse dit indlæg på mere end én måde...

Måde 1:
Du stopper, når du har vundet én gang. Dermed kan projektet max køre 8 hænder, da du enten har vundet inden det tidspunkt eller tabt alt. I det tilfælde kommer du selvfølgelig aldrig op på 15 hænder, men i så fald er din chance 1-0.42% = 99.58%. Dvs du taber 1 ud af 236 gange.

Måde 2:
Du vil aldrig risikere at komme op på mere end 15 spil, så hvis du vinder hånd nr 8 (eller en senere hånd), så stopper du. Så tror jeg, at udregningen bliver den samme. Du undlader blot at starte en ny, hvor du ikke kan nå at spille 8 i træk (dvs fra hånd nr 9 og op til hånd nr 15). Risikoen for at ramme en 8-losing-streak er dermed den samme, for du kunne jo alligevel ikke ramme en 8-losing-streak i udregningen.

Så jeg vil stadig mene, at din risiko er 1 ud af 30 gange.

-----

Rent intuitivt giver det jo også god mening, for ved måde 1 giver du det 1 forsøg og taber 1 ud af 240 gange (roughly), og i måde 2 giver du det 8 forsøg og taber 1 ud af 30 gang, hvilket er 1/8 del af de 240 gange...

Man kan naturligvis ikke regne det ud præcist på den måde, men det giver stadig et cirkatal, som viser, at det nok ikke er en helt forkert udregning :)

So to sum up... Don't do it! ;)

Du vinder måske et lille beløb, men taber måske et kæmpe... Og risikoen for at tabe er stor nok til, at det slet ikke kan betale sig med de smågevinster... Hverken matematisk eller i praksis :)

@roedroed

Du læser jo ikke, hvad manden skriver..

1 - I regner ud fra forkerte tal. Der er ca 42% chance for en win, 8% for push, 49% for loss. Edgen er noget bedre, end disse tal viser, da man hyppigt vinder mere end 1 bet når man vinder.

2 - Hvis decket ikke er uendeligt, er chancen for at vinde lige efter man har vundet faktisk en lille smule mindre end hvis man lige har tabt. I har sikkert hørt om at tælle kort. Dette virker netop, fordi sammensætningen af decket ændrer sig. Når man lige har vundet, har man sandsynligvis lige "brugt" nogle af de gode kort. Det gør nok ikke den helt store forskel, men hænder i BJ er ikke uafhængige.

wizardofodds.com/games/blackjack/appendix/4/

@Jörn

Det er cirkabetragtninger. Jeg er klar over, at det ikke er præcist... Men ud fra en tilbagebetaling på lige under 100%, så må det være fair nok at tillægge sig en hand win percentage på lige under 50%. Du argumenterer for, at den er lavere, da pushdelen udgør en stor del og den ser vi bort fra. Det er meget muligt, men det gør det bare endnu værre (for så skulle vi regne med 46%, hvilket er de 42 + det halve af pushdelen, i stedet for 49.5%) :)

Det er ikke præcist... Men omvendt er det vel heller ikke nødvendigt med en præcis udregning. Vi ved jo godt, at resultatet bliver negativt og dårligt... Så om han får at vide, at det er 1 ud af 119 eller 1 ud af 109 er nok ikke altafgørende for OP's overvejelser.

Og ja, spillet ændrer sig marginalt, hvis der ikke blandes ind imellem. Nu kunne jeg forestille mig, at det var online, at OP ville spille, og uden at vide det, så kunne jeg sagtens forestille mig, at der blandes ind imellem. Uanset hvad, så er det nok ikke muligt at skabe en kæmpe edge derigennem, så den smule udsving vælger jeg ligeledes at se bort fra.

Så ja, det er cirkatal, men et fint estimat i mine øjne. Der er ikke behov for helt eksakte (hvilket i øvrigt en kræve en uforholdsmæssig stor udregning for at finde frem til dem). I teorien har du naturligvis ret. Jeg mener bare ikke, at det er så praktisk relevant for den oplysning, OP ønsker :)

Men udregning med 46% giver:

0.54^8 = 0.72%

1-(0.9928^8) = 5.62% eller 1 ud af 18 gange (i stedet for de 1 ud af 30 gange). Så antager vi, at man spiller videre efter ethvert push med samme indsats for at få hånden afgjort.

Don't Jonas, just don't :-)

jannik_pro skrev:
Don't Jonas, just don't :-)

hold da op, der er vel for helvede ikke nogen der har prøvet at komme på et casino, uden at de ikke har tænkt Martin Gale. :) :)
Men ja tab er sikkert