Hej PN.
Sidder og rodder lidt rundt med udregninger af turneringsvarians.
Det jeg gerne vil nå frem til er f.eks. 5% risiko for downswing af X buyin størrelse i en given turnering over et givent antal turneringer. Så grundlæggende er det vel en normalfordeling jeg spørger efter.
Det må være logisk at variansen afhænger af
Buyin(stake+rake)
Payout-struktur (Stejlere payout struktur giver mulighed for større downswing)
Ens "sande" ROI (som et udtryk for ens skillforskel i forhold til gennemsnittet af feltet)
Antal deltagere i turnering (større turneringsfelter må nødvendigvis give mulighed for større downswing)
Antal turneringer i sample (Klart, at man maksimalt kan have et 100 buyin downswing, hvis sample er 100 turnering; men må også være sådan, at hvis man har positiv ROI, er et downswing over en sample på enormt mange turneringer så godt som umuligt)
Er der nogen, der er stødt på en model for, hvordan disse faktorer hænger sammen og hvilke, der vejer mest?
F.eks. Er der risiko for et absolut (altså i $) større downswing i en
109$ turnering med 200 deltagere, man spiller 1000 gange, hvor ens sande ROI er 15%
end der er i en
55$ turnering med 1400 deltagere, man spiller 1000 gange, hvor ens sande ROI er 25%
BTW. Jeg påstår ikke her, at min ROI i 109 dollar turneringer er 15%!
Mange hilsner
/J
Udregning af varians
Mener at denne er en af dem med bedst info omkring Tourvarians, du kan jo så selv ændre lidt på de bagved liggende tal.
Buyin betyder sådan set ikke i sig selv noget for hvor varianspræget en turnering er. Men den en dyrere tour tager en større bid af rullen, når der ikke cashes i en periode.
Jeg plejer at google "one thousand Shaun Deebs", når jeg vil genlæse det, der har givet mig en forståelse for varians i MTTs.
Der er lidt tal og lidt udregning og nogle grafer. Måske kan det give dig en ide. Der er også referencer til mere data og flere udregning. Du må selv ligge og rode med det. Jeg tror ikke du kan få alle de oplysninger du skal bruge fra kun denne side, men det kan måske hjælpe.
http://www.nsdpoker.com/2011/01/mtt-pros/
Edit: Jeg kan se Farre har skrevet det samme.
Der er obv risiko for et størst absolut $ downswing i scenarie 1, da det jo er fysisk muligt at tabe samtlige tours du spiller selvom du er vindende. Omend sandsynligheden for at du taber 1000 tours i streg, med en roi på 15% er nærmest ikke eksisterende.
Der er størst sandsynlighed for et downswing i scenarie 2.
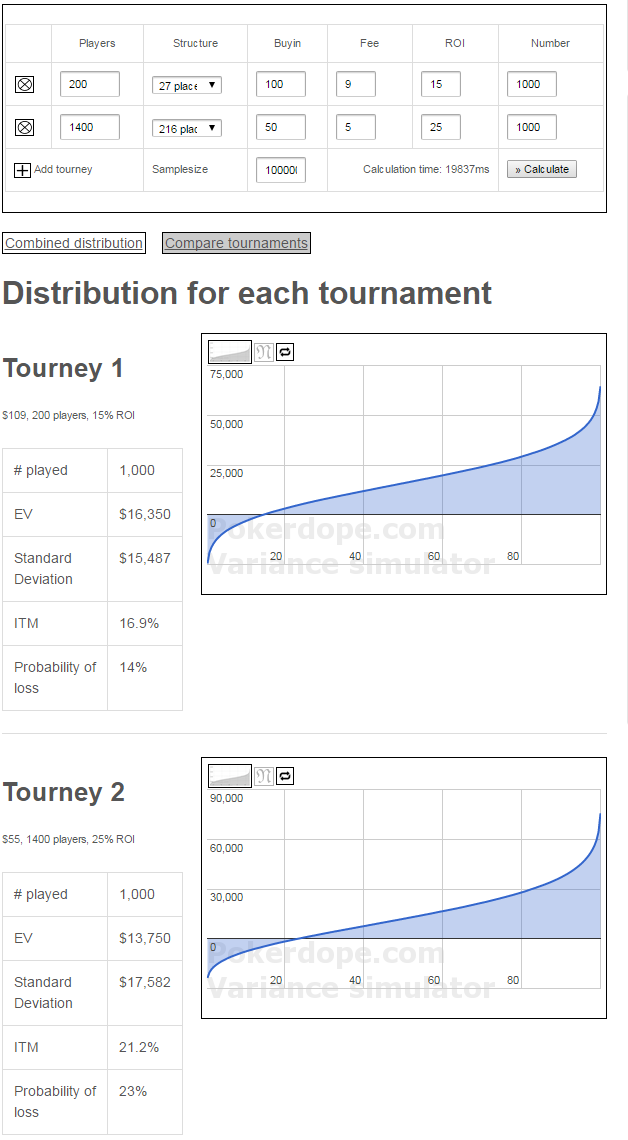
Tjek evt den her ud: http://pokerdope.com/tournament-variance-calculator/
Argyle_DK skrev:Buyin betyder sådan set ikke i sig selv noget for varianspræget en turnering er. Men den en dyrere tour tager en større bid af rullen, når der ikke cashes i en periode.
Jeg plejer at google "one thousand Shaun Deebs", når jeg vil genlæse det, der har givet mig en forståelse for varians i MTTs.
Der er lidt tal og lidt udregning og nogle grafer. Måske kan det give dig en ide. Der er også referencer til mere data og flere udregning. Du må selv ligge og rode med det. Jeg tror ikke du kan få alle de oplysninger du skal bruge fra kun denne side, men det kan måske hjælpe.
http://www.nsdpoker.com/2011/01/mtt-pros/
Edit: Jeg kan se Farrea
Hey Argyle.
Har læst den før, og den er bestemt interessant. Men den er også ret problematisk at tage som udtryk for en generel model for udregning af varians, da den er lavet over én spillers trods alt relative lille sample af turneringer af meget forskellig størrelse.
Omkring hans metode skriver han
used Shaun’s results from January 2009 to present on Stars and FTP. I filtered for buy-ins between $55 and $216 and included only NLHE tourneys with at least 181 entrants. OPR doesn’t record rebuys, so I removed rebuy tourneys. This left 3,049 tourneys with an average buy-in of $119.72 in which Deeb earned $294,027 with an awesome ROI of 81% and an ITM of 11.5%. Obviously, not many people can play or run as well as Shaun Deeb, but these results provide a starting point.
But, say you’re not Shaun Deeb. I can make a lower ROI player by simply taking Shaun’s distribution and lowering the payouts. (For an ROI of x, multiply the prizes by (1+x)*0.554 .) This isn’t very accurate, but it’s good enough for my purposes (especially since Shaun has a low ITM%). Here’s the 1,000 tourney histogram for a 20% ROI player:
Det links, der er på siden til blandt andet denne.
http://www.nsdpoker.com/mtt-data/
virker ved første øjekast interessant, men igen linker han i sit "metodeafsnit" direkte tilbage til, at det er Shaun Deeps relativt lille sample, der er brugt til at danne en model.
Men mange tak :)
Der er obv risiko for et størst absolut $ downswing i scenarie 1, da det jo er fysisk muligt at tabe samtlige tours du spiller selvom du er vindende. Omend sandsynligheden for at du taber 1000 tours i streg, med en roi på 15% er nærmest ikke eksisterende.
Der er størst sandsynlighed for et downswing i scenarie 2.
Tjek evt den her ud: http://pokerdope.com/tournament-variance-calculator/
Hej Totter.
Ja det var dumt formuleret af mig; det med absolut største downswing. Det er klart, at det er der, hvor man spiller for flest penge, som du skriver :)
Jeg er grundlæggende ret ligeglad i min bankroll management med hvad risikoen er for at tabe (altså der hvor kurven skærer Y aksen), jeg er langt mere interesseret i hvor stort tabte kan forventes at være; lad os f.eks sige de 5% af gangene, det går dårligst. Der giver poker tournament calculator et bud, men jeg er ret sikker på, at modellen er fejlagtig, da den slet ikke tilskriver field size nok betydning.
Et eksempel er 2 slags 109 dollar turneringer begge med ROI på 15 procent og udbetaling til 12 procent over 1000 turnering med henholdsvis 200 og 2000 deltagere.
Der er 5 percentilen (Altså den ene gang det går dårligst ud af 20) henholdsvis -5,4k$ og -7,7k$ og det er simpelthen fuldstændigt umuligt for mig at tro på, at field size ikke skulle betyde mere end det.
Det irriterer mig også ret meget, at de ikke skriver hvordan formlen fungerer, da de tydeligvis har lavet en formel, der indeholder de elementer jeg skrev i mit open.
Men tak :)
Mvh
/J
Hmm, jeg får de her resultater (godt nok med hhv 14% og 15% udbetaling, kunne ikke vælge 12%??);
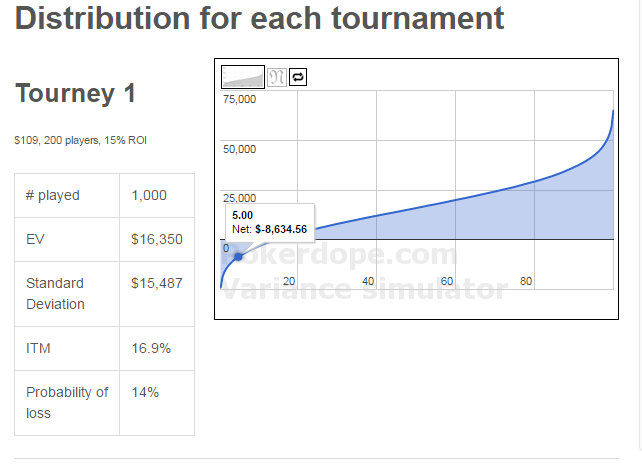
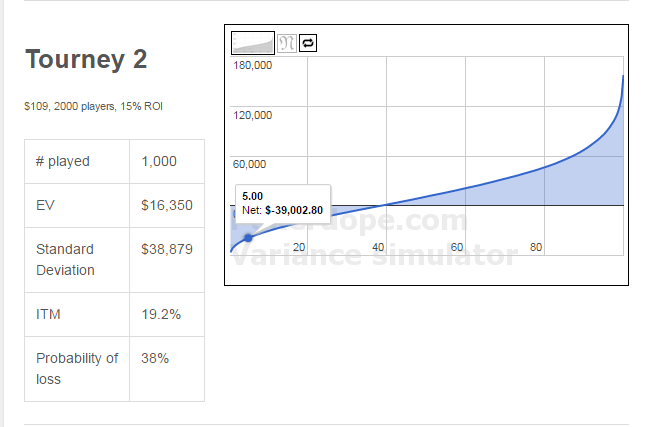
Totter89 skrev:Hmm, jeg får de her resultater (godt nok med hhv 14% og 15% udbetaling, kunne ikke vælge 12%??);
Det var sgu mærkeligt.
Så må jeg have tastet noget forkert ind før - PINLIGT!
Det virker jo meget mere sandsynligt, at den model de bruger, så er tilnærmelsesvist korrekt - Fedt! Ville stadig være ret interesseret i at se formlen, der ligger bag, men jeg kan selvfølgelig bare sætte en masse forskellige scenarier op og ekstrapolere den ud fra det.
Takker og undskylder min sløsethed.
Mvh
/J